「オイラーの公式」の活用例
これまで、【コイルのインピーダンスの計算式「\(Z_L =j \omega L\) 」の求め方(4)】の投稿などで「オイラーの公式」の説明に挑戦したり、使ったりしましたが、ここではその他の「オイラーの公式」の活用例を二つ書きます。
「極座標」上の掛け算
最初に書くのは、「極座標」上での数値の掛け算です。
以前の投稿で、「極座標」同士の掛け算が下記になると書きました。
$$(100V_{rms}∠0deg) \times (1.15A_{rms}∠30deg) = 115VA∠30deg $$
この計算が正しいことを、「オイラーの公式」を使って説明します。
この計算は、【電流や電力などの「極座標」を「複素平面」で表示〔2〕(抵抗とコンデンサー)】の投稿で行いましたが、その投稿に書いた「極座標」上の掛け算のルールは、『矢印の長さはそのまま掛け合わせ、「\(∠\) 」で表す位相(角度)は足し合わせます。』でした。
ここでは、「極座標」上での掛け算のルールがこうなることを、「オイラーの公式」を使って説明します。
「オイラーの公式」は下の式でした。
$$e^ {j x} = \cos x + j \sin x$$
「\(j\) 」は虚数単位「\(i=\sqrt{-1}\) 」のことで、電気の計算では電流の記号「\(i\) 」と区別するために「\(j\) 」を使います。
以下は「おさらい」ですが、少し長くなったので、結果だけを知りたい方は、下の方の「さて、ここからが今回の本題です。」からお読みください。
まずは、【電流や電力などの「極座標」を「複素平面」で表示〔2〕(抵抗とコンデンサー)】で書いた内容を書きます。
想定する回路を下に示します。
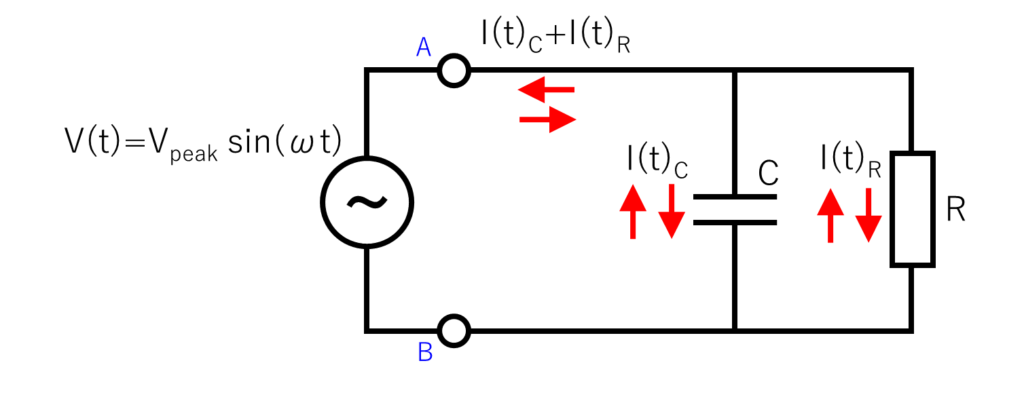
・電圧振幅\((V_{peak}):141V\) ( ⇒実効値\(:100V_{rms}\))
・抵抗値\((R):100Ω\)
・容量値\((C):18.4\mu F\) (マイクロファラッド)
・周波数\((f):50Hz\) (\(\omega=2\pi f\) )
下のグラフは、上の回路図の左端の「交流電圧源:\(V(t)\) 」の「実効電圧値:\(100V_{rms}\) 」と「位相:\(0deg\) 」を表すグラフです。
左下の極座標グラフの青色の矢印は、実効電圧値と位相が「\(100V_{rms}∠0deg\) 」であることを表します。
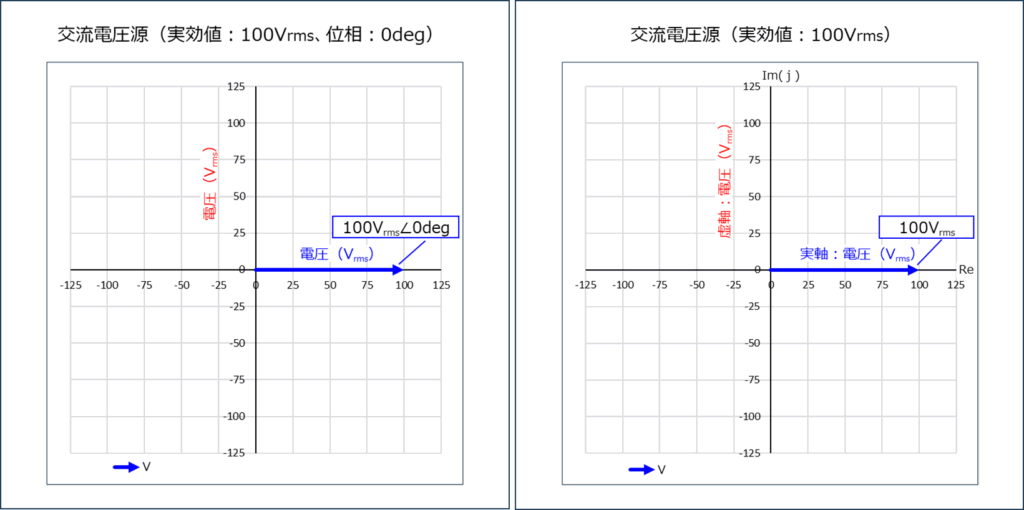
右側のグラフは複素平面のグラフで、青色の矢印は「\(100V_{rms}+j0V_{rms}\) 」を表します。
次に下のグラフは、「抵抗」と「コンデンサー」に流れる電流「\(I(t)=I(t)_C+I(t)_R\) 」を表します。
左下の極座標グラフの紫色の矢印は、実効電流値と位相が「\(1.15A_{rms}∠30deg\) 」になることを表します。
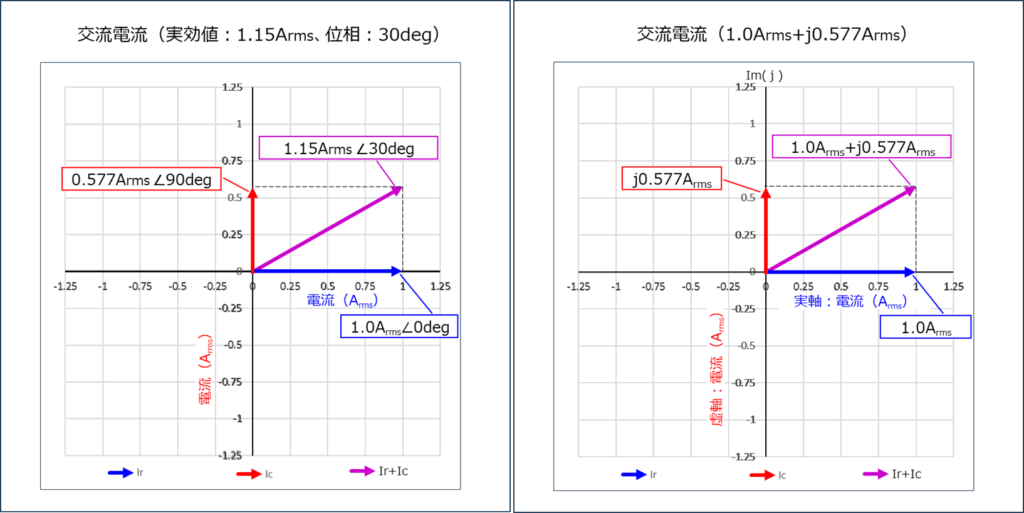
右側のグラフは複素平面のグラフで、紫色の矢印は「\(1.0A_{rms}+j0.577A_{rms}\) 」を表します。
最後に、電圧と電流を掛けて、下のように電力を計算しました。
$$V \times I = (100V_{rms}\angle 0deg) \times (1.15A_{rms}\angle 30deg) $$
$$ = (100V_{rms} \times 1.15A_{rms}) \angle (0deg+30deg) $$
$$ = 115VA\angle 30deg $$
この計算結果は、左下の極座標の紫色の矢印を表します。
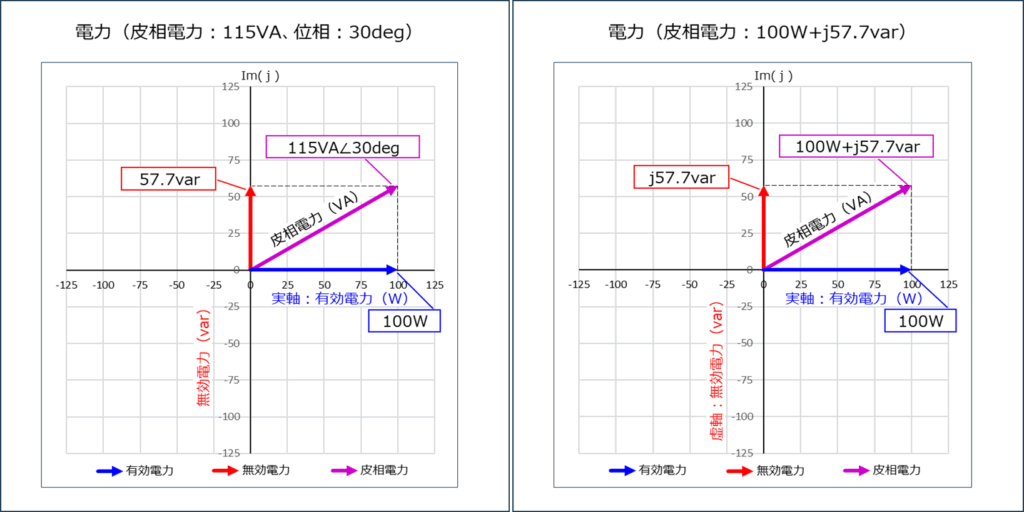
繰り返しになりますが、右側のグラフは複素平面のグラフで、このグラフの紫色の矢印は「\(100W+j57.7var\) 」を表します。
複素数での計算は、下記になります。
$$V \times I=(100V_{rms} + j0V_{rms}) \times (1.0A_{rms}+j0.577A_{rms}) $$
$$ =100V_{rms} \times (1.0A_{rms}+j0.577A_{rms}) $$
$$=(100V_{rms} \times 1.0A_{rms}) +j(100V_{rms} \times 0.577A_{rms}) $$
$$=100W+j57.7var$$
少し長くなりましたが、【電流や電力などの「極座標」を「複素平面」で表示〔2〕(抵抗とコンデンサー)】に書いたのは、こんな内容でした。
さて、ここからが今回の本題です。
極座標上の「\(A∠\theta_A\) 」と「\(B∠\theta_B\) 」の掛け算は、下記になると書きました。
$$A∠\theta_A \times B∠\theta_B$$
$$= (A \times B)∠(\theta_A + \theta_B)$$
こう書きながらも、「\(∠\) 」の左側は掛け算で、右側は足し算になるというのは、ちょっと疑問でした。
その疑問は、「オイラーの公式」を使って説明できることが分かったので、そのことを書きます。
「オイラーの公式」は下記です。
$$e^ {j x} = \cos x + j \sin x$$
まずは下の「極座標」の掛け算の式から始めます。
$$A∠\theta_A \times B∠\theta_B$$
上の式を、複素数の式で表すと下記になります。
$$A∠\theta_A \times B∠\theta_B$$
$$ = (A \cos \theta_A +j A \sin \theta_A) \times (B \cos \theta_B +j B \sin \theta_B) $$
$$= A (\cos \theta_A +j \sin \theta_A) \times B (\cos \theta_B +j \sin \theta_B) $$
この三角関数の式を、「オイラーの公式」を使って指数関数の式にすると下記になるので、そのまま計算していきます。
$$ A (\cos \theta_A +j \sin \theta_A) \times B (\cos \theta_B +j \sin \theta_B) $$
$$= A (e^ {j \theta_A}) \times B (e^ {j \theta_B}) $$
$$= (A \times B) (e^ {j \theta_A} \times e^ {j \theta_B}) $$
$$= (A \times B) e^ {(j \theta_A + j \theta_B)} $$
$$= (A \times B) e^ {j (\theta_A + \theta_B)} $$
ここで再び「オイラーの公式」を使って、上の指数関数の式を三角関数の式に戻すと下記になります。
$$ (A \times B) e^ {j (\theta_A + \theta_B)} $$
$$= (A \times B) (\cos (\theta_A + \theta_B) + j\sin (\theta_A + \theta_B)) $$
上の式を、「極座標」の「矢印の長さ」と「角度」で表すと下記になります。
$$(A \times B) ∠ (\theta_A + \theta_B)$$
これで、極座標上の掛け算は、下のように計算できることが分かりました。
$$(A∠θ_A) \times (B∠θ_B)=(A \times B) ∠ (\theta_A + \theta_B)$$
さて、次の項では「オイラーの公式」を使って、三角関数の「加法定理」を導いてみます。
三角関数の「加法定理」の導出
今回、「オイラーの公式」を使って導く三角関数の「加法定理」は下記です。
$$\sin (\alpha+\beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta $$
$$\cos (\alpha+\beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta $$
「オイラーの公式」を下に書きます。
$$e^ {j x} = \cos x + j \sin x$$
この「オイラーの公式」の左辺の「\(x\) 」に、「\(\alpha + \beta \) 」を入れます。
$$ e^ {j x} = e^ {j (\alpha + \beta)} $$
$$ = e^ {j \alpha + j \beta} $$
$$ = e^ {j \alpha} e^ {j \beta} $$
ここで、「オイラーの公式」を使って、右辺を指数関数から三角関数にします。
$$e^ {j (\alpha + \beta)} = e^ {j \alpha} e^ {j \beta}$$
$$ = (\cos \alpha + j \sin \alpha) (\cos \beta + j \sin \beta) $$
$$ = \cos \alpha (\cos \beta + j \sin \beta) + j \sin \alpha (\cos \beta + j \sin \beta) $$
$$ = \cos \alpha \cos \beta + j \cos \alpha \sin \beta + j \sin \alpha \cos \beta + jj \sin \alpha \sin \beta $$
$$ = \cos \alpha \cos \beta + j \cos \alpha \sin \beta + j \sin \alpha \cos \beta - \sin \alpha \sin \beta $$
上の式を、実数部分を左、虚数部分を右に集めると下記になります。
$$e^ {j (\alpha + \beta)} = (\cos \alpha \cos \beta - \sin \alpha \sin \beta) + j (\sin \alpha \cos \beta + \cos \alpha \sin \beta) $$
また、「オイラーの公式」の「\(x\) 」に「\(\alpha + \beta \) 」を入れると、下の式のようにも表せます。
$$e^ {j (\alpha + \beta)} = \cos (\alpha + \beta) + j \sin (\alpha + \beta) $$
上の二つの式の左辺は両方「\(e^ {j (\alpha + \beta)}\) 」なので、右辺同士を等号でつなぐと下記になります。
$$ \cos (\alpha + \beta) + j \sin (\alpha + \beta) = (\cos \alpha \cos \beta - \sin \alpha \sin \beta) + j (\sin \alpha \cos \beta + \cos \alpha \sin \beta)$$
上の式において、虚数同士は等しくなるので、下の式が成り立ちます。
$$ j \sin (\alpha + \beta) = j (\sin \alpha \cos \beta + \cos \alpha \sin \beta) $$
$$ \sin (\alpha + \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta $$
同様に、実数同士も等しくなるので、下の式も成り立ちます。
$$ \cos (\alpha + \beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta $$
このように、「オイラーの公式」から、三角関数の「加法定理」の式を導くことができます。
この「加法定理」から、「倍角の公式」や「和積/積和公式」を導くこともできるので、もしものときに役立つかもしれません。
美しい等式
「オイラーの公式」の活用例ではないのですが、「オイラーの公式」から導ける「世界一美しい等式」と言われる式があります。
その「世界一美しい等式」は下記です。
$$e^ {j \pi} +1=0$$
下記の方が良いという方もいます。
$$e^ {j \pi} = -1 $$
美しいと感じるかは別として、「\(e\) 」「\(j\) 」「\(\pi\) 」と、「\(1\) 」「\(0\) 」または「\(-1\) 」という無関係な数の間に、このようなシンプルな等式が成り立つのは、やはり不思議な感じはします。
この等式は、「オイラーの公式」の「\(x\) 」に「\(\pi\) 」を入れると、下のように簡単に導けます。
$$e^ {j x} = \cos x + j \sin x$$
$$e^ {j \pi} = \cos \pi + j \sin \pi$$
$$e^ {j \pi} = (-1) + j 0$$
$$e^ {j \pi} = -1 $$
$$e^ {j \pi} +1= 0$$
この等式自体を、何かに活用できることは無いと思いますが、やはり不思議です。
「オイラーの公式」はシンプルなので、覚えておくと何かの役に立つかもしれません。
よろしければ以下のバナーをクリックしていただけると励みになります!
にほんブログ村
科学ランキング

