直流と交流の違い〔９〕（交流電源の消費電力の計算式）

前回の投稿の最後に「小技を使いながら計算してみます」と書きましたが、ちょっと失礼な書き方だったと反省しています。

自分の力でまともには計算できそうにないので、数学の公式を使ったりしながら計算していきます。

「sin² α」を「cos β」で表す

これから計算していく式は、下の式になります。

$$E=\lim_{n \to ∞}\sum_{k=1}^{n} \left(\displaystyle\frac{\left(V_ {peak} \sin \left(\omega \displaystyle\frac{kT}{n} \right) \right)^{2}}{R} ✕ \displaystyle\frac{T}{n} \right)$$

この式は電力量（＝エネルギー）を計算する式なので、エネルギーを表す「\(E=\)」としました。

この式を少し変形すると下記になります。

$$E=\displaystyle\frac{{V_ {peak}}^{2} T}{R} \lim_{n \to ∞}\sum_{k=1}^{n} \displaystyle\frac{1}{n} \sin^{2} \left(\omega \displaystyle\frac{kT}{n} \right)$$

本当はこの式を、下のようにして計算していきたかったのですが、自分には無理でした。

$$E=\displaystyle\frac{{V_ {peak}}^{2} T}{R} \lim_{n \to ∞} \displaystyle\frac{1}{n} \left( \sin^{2} \left(\omega \displaystyle\frac{1T}{n} \right)+\sin^{2} \left(\omega \displaystyle\frac{2T}{n} \right)+...+\sin^{2} \left(\omega \displaystyle\frac{nT}{n} \right) \right)$$

べき級数展開を使うと解けるのでしょうか。

いつか、挑戦してみたいと思います。

さて、余計なことを書きましたが、一つ前の式に戻ります。

ここでは、「\(\sin^2 α\)」を「\(\cos β\)」で表す公式：2倍角の公式を使います。

今回使用する公式は下記になります。

$$\cos 2x=1-2\sin^2 x$$

この式を少し変形します。

$$\sin^2 x=\displaystyle\frac{1-\cos 2x}{2}$$

これを使って一つ前の式を書き換えると下記になります。

$$E=\displaystyle\frac{{V_ {peak}}^{2} T}{R} \lim_{n \to ∞}\sum_{k=1}^{n} \displaystyle\frac{1}{n} \sin^{2} \left(\omega \displaystyle\frac{kT}{n} \right)$$

$$=\displaystyle\frac{{V_ {peak}}^{2} T}{R} \lim_{n \to ∞}\sum_{k=1}^{n} \displaystyle\frac{1}{n} \left(\displaystyle\frac{1-\cos \left(2\omega \displaystyle\frac{kT}{n} \right)}{2}\right)$$

$$=\displaystyle\frac{{V_ {peak}}^{2} T}{2R} \lim_{n \to ∞}\sum_{k=1}^{n} \displaystyle\frac{1}{n} \left(1-\cos \left(2\omega \displaystyle\frac{kT}{n} \right)\right)$$

$$=\displaystyle\frac{{V_ {peak}}^{2} T}{2R} \lim_{n \to ∞}\sum_{k=1}^{n} \left(\displaystyle\frac{1}{n}-\displaystyle\frac{1}{n}\cos \left(2\omega \displaystyle\frac{kT}{n} \right)\right)$$

$$=\displaystyle\frac{{V_ {peak}}^{2} T}{2R} \left(\lim_{n \to ∞}\sum_{k=1}^{n} \displaystyle\frac{1}{n} -\lim_{n \to ∞}\sum_{k=1}^{n} \displaystyle\frac{1}{n} \cos \left(2\omega \displaystyle\frac{kT}{n} \right)\right)$$

ここまでで、何とか「\(\sin^2 α\)」を「\(\cos β\)」で表す式にできました。

ここからは、大きい（ ）内の前半部分を\(E_F\)、後半部分を\(E_B\)として別々に解いていきます。

大きい（ ）内の前半分：EFの計算

大きい（ ）内の前半部分：\(E_F\)を下記に示します。

$$E_F=\displaystyle\frac{{V_ {peak}}^{2} T}{2R} \lim_{n \to ∞}\sum_{k=1}^{n} \displaystyle\frac{1}{n} $$

まずは、これを解いていきます。

$$E_F=\displaystyle\frac{{V_ {peak}}^{2} T}{2R} \lim_{n \to ∞}\sum_{k=1}^{n} \displaystyle\frac{1}{n} $$

$$E_F=\displaystyle\frac{{V_ {peak}}^{2} T}{2R} \lim_{n \to ∞} \left(\displaystyle\frac{1}{n} +\displaystyle\frac{1}{n} +...+\displaystyle\frac{1}{n} \right)$$

上の式では、n個の「\(\displaystyle\frac{1}{n}\)」を足しているので下記になります。

$$E_F=\displaystyle\frac{{V_ {peak}}^{2} T}{2R} \lim_{n \to ∞} \left(\displaystyle\frac{1}{n} +\displaystyle\frac{1}{n} +...+\displaystyle\frac{1}{n} \right)$$

$$=\displaystyle\frac{{V_ {peak}}^{2} T}{2R} \lim_{n \to ∞} \left(\displaystyle\frac{n}{n} \right)$$

$$=\displaystyle\frac{{V_ {peak}}^{2} T}{2R} \lim_{n \to ∞} \left(1 \right)$$

$$=\displaystyle\frac{{V_ {peak}}^{2} T}{2R} $$

大きい（ ）内の前半部分：\(E_F\)の計算はここまでにします。

大きい（）内の後半部分：EBの計算

大きい（ ）内の後半部分：\(E_B\)を下記に示します。

$$E_B=\displaystyle\frac{{V_ {peak}}^{2} T}{2R} \left(\lim_{n \to ∞}\sum_{k=1}^{n} \displaystyle\frac{1}{n} \cos \left(2\omega \displaystyle\frac{kT}{n} \right)\right)$$

この式の交流波形としての意味が分かりやすいように、「\(\omega\)」を「\(\pi\)」と「\(T\)」で表す式にします。

$$\omega=2\pi f$$

$$=2\pi \displaystyle\frac{1}{T}$$

前回の投稿で書きましたが、「\(T\)」は家庭用電源の周波数を50Hz（東日本）としたときの周期で、具体的には「20ms」になります。

この式を上の式に入れて計算してみます。

$$E_B=\displaystyle\frac{{V_ {peak}}^{2} T}{2R} \left(\lim_{n \to ∞}\sum_{k=1}^{n} \displaystyle\frac{1}{n} \cos \left(2\omega \displaystyle\frac{kT}{n} \right)\right)$$

$$=\displaystyle\frac{{V_ {peak}}^{2} T}{2R} \left(\lim_{n \to ∞}\sum_{k=1}^{n} \displaystyle\frac{1}{n} \cos \left(2\left( 2\pi \displaystyle\frac{1}{T}\right) \displaystyle\frac{kT}{n} \right)\right)$$

$$=\displaystyle\frac{{V_ {peak}}^{2} T}{2R} \left(\lim_{n \to ∞}\sum_{k=1}^{n} \displaystyle\frac{1}{n} \cos \left(\displaystyle\frac{4\pi k}{n} \right)\right)$$

大きい（ ）内の後半部分：\(E_B\)の計算はここまでにします。

EFとEBの説明と計算

\(E_F\)と\(E_B\)を元の式に戻すと下記になります。

$$E=\displaystyle\frac{{V_ {peak}}^{2} T}{2R} +\displaystyle\frac{{V_ {peak}}^{2} T}{2R} \left(\lim_{n \to ∞}\sum_{k=1}^{n} \displaystyle\frac{1}{n} \cos \left(\displaystyle\frac{4\pi k}{n} \right)\right)$$

これは周期：\(T\)（20ms）における電力量を表す式なので、\(T\)で割り算すると下記の電力を表す式になります。

$$P_{AC}(t)=\displaystyle\frac{{V_ {peak}}^{2} }{2R} +\displaystyle\frac{{V_ {peak}}^{2}}{2R} \left(\lim_{n \to ∞}\sum_{k=1}^{n} \displaystyle\frac{1}{n} \cos \left(\displaystyle\frac{4\pi k}{n} \right)\right)$$

この式の意味を下のグラフで確認します。

まず下のグラフは、家庭用交流電源（50Hz）の電圧変化を表しています。

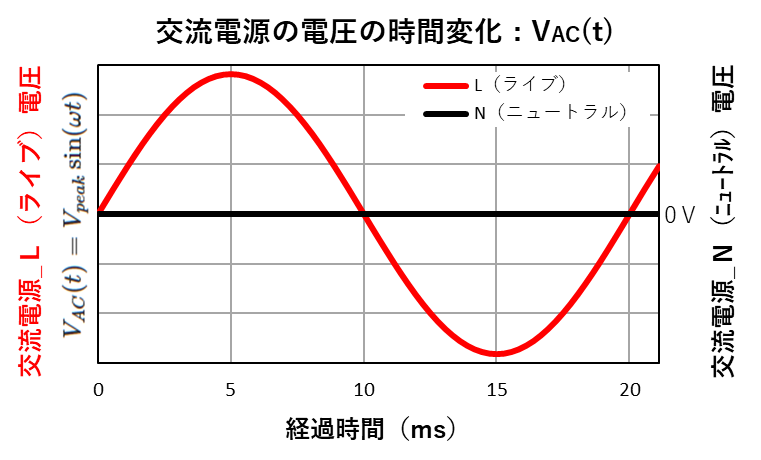
次に下のグラフは、上のグラフに対応した消費電力の変化を表しています。

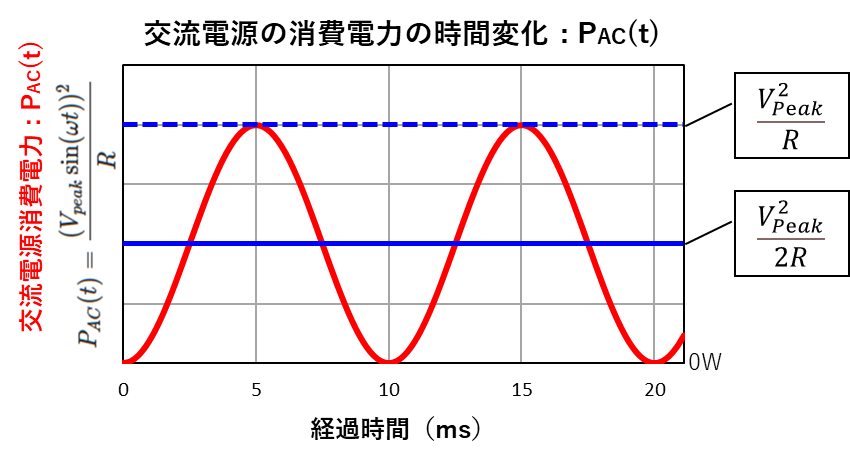
上の式をもう一度書きますが、前半部分の\(\left(\displaystyle\frac{{V_ {peak}}^{2} }{2R}\right) \)は、上のグラフの青い実線を表しています。

$$P_{AC}=\displaystyle\frac{{V_ {peak}}^{2} }{2R} +\displaystyle\frac{{V_ {peak}}^{2}}{2R} \left(\lim_{n \to ∞}\sum_{k=1}^{n} \displaystyle\frac{1}{n} \cos \left(\displaystyle\frac{4\pi k}{n} \right)\right)$$

次に後半部分の\(\left(\displaystyle\frac{{V_ {peak}}^{2}}{2R} \left(\lim_{n \to ∞}\sum_{k=1}^{n} \displaystyle\frac{1}{n} \cos \left(\displaystyle\frac{4\pi k}{n} \right)\right)\right) \)ですが、先ほどの青い実線を軸に上下する波型の赤い実線を表しています。

「\(\cos\)」の中が「\(4\pi\)」になっているので、赤い実線が上下を2回繰り返している点にも着目してください。

この二つの式を足し合わせると、上のグラフの赤い実線になります。

このグラフの赤い線の動きからも分かるように、\(\left(\displaystyle\frac{{V_ {peak}}^{2}}{2R} \left(\lim_{n \to ∞}\sum_{k=1}^{n} \displaystyle\frac{1}{n} \cos \left(\displaystyle\frac{4\pi k}{n} \right)\right)\right) \)は、青い実線を中心に上側と下側の面積が等しいので、合計するとプラスとマイナスでゼロになり、結局青い線の式だけが残ります。

そのため、上の式は下記になります。

$$P_{AC}=\displaystyle\frac{{V_ {peak}}^{2} }{2R} +0$$

$$=\displaystyle\frac{{V_ {peak}}^{2} }{2R} $$

できるだけ電圧や電力、電力量といった物理量との関係が伝わるようにと思い、少し回りくどい説明になりました。

積分を使用すると、もっとシンプルに求めることができるので、次回はそれに触れながら、最終的に「100V」と「141V」の関係を書こうと思います。

よろしければ以下のバナーをクリックしていただけると励みになります！

にほんブログ村
人気ブログランキング