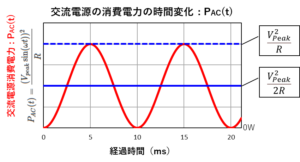
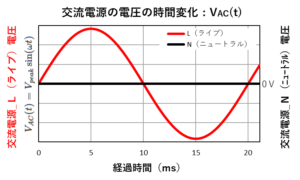
直流と交流の違い〔１０〕（積分で求める交流電源の消費電力計算式）

2023年11月28日 2023年12月19日

講師Kazu

前回の投稿で、「積分を使用すると、もっとシンプルに求めることができる」と書きましたが、思っていたよりも長くなってしまいました。

そのため今回は、積分の計算までにします。

積分を使った式への変更

最初に下の式ですが、前回投稿の最初に書いた計算式です。

$$E=\lim_{n \to ∞}\sum_{k=1}^{n} \left(\displaystyle\frac{\left(V_ {peak} \sin \left(\omega \displaystyle\frac{kT}{n} \right) \right)^{2}}{R} ✕ \displaystyle\frac{T}{n} \right)$$

前回投稿では、上の式を変形して下の式にしました。

$$E=\displaystyle\frac{{V_ {peak}}^{2} T}{2R} \left(\lim_{n \to ∞}\sum_{k=1}^{n} \displaystyle\frac{1}{n} -\lim_{n \to ∞}\sum_{k=1}^{n} \displaystyle\frac{1}{n} \cos \left(2\omega \displaystyle\frac{kT}{n} \right)\right)$$

ずいぶん前ですが、「$\lim \sum $」の式は下のように積分でも表せると書きました。

$$移動距離=\lim_{n \to ∞}{\sum_{k=1}^{n} at_k}Δt=\int{at}\, dt$$

この式は、加速度：aと時間：tから移動距離を求める式です。

この関係を使って、今回の式を積分で表します。

まず最初に、上の式の左側にある「$T$」を右側の大カッコの中に戻して「$\displaystyle\frac{T}{n}$」のかたちにします。

$$=\displaystyle\frac{{V_ {peak}}^{2} }{2R} \left(\lim_{n \to ∞}\sum_{k=1}^{n} \displaystyle\frac{T}{n} -\lim_{n \to ∞}\sum_{k=1}^{n} \cos \left(2\omega \displaystyle\frac{kT}{n} \right)\displaystyle\frac{T}{n}\right)$$

「$\displaystyle\frac{T}{n}$」は、周期「$T$ 」を「$n \to ∞$」で割り算するので非常に短い時間「$\Delta t$ 」になり、積分の式では「$dt$」になります。

次に「$\displaystyle\frac{kT}{n}$」ですが、これは周期「$T$ 」を「$n$ 」分割し、その「$1$ 」番目から「$n$ 」番目までの時間を表すので、これは経過時間「$t$ 」に置き換えられます。

そうすると、上の式は下の積分の式で表せます。

$$E=\displaystyle\frac{{V_ {peak}}^{2} }{2R} \left(\lim_{n \to ∞}\sum_{k=1}^{n} \displaystyle\frac{T}{n} -\lim_{n \to ∞}\sum_{k=1}^{n} \cos \left(2\omega \displaystyle\frac{kT}{n} \right)\displaystyle\frac{T}{n}\right)$$

$$=\displaystyle\frac{{V_ {peak}}^{2} }{2R} \left(\int_{0}^{T} \, dt -\int_{0}^{T} \cos 2\omega t \, dt \right)$$

「$\int$ 」の上下の「$0$」と「$T$」は積分の範囲を表しており、「$T$」は交流波形の周期で、具体的には0～20msになります。

数学的には、いろいろと正確でない表現があると思いますが、ここでは大目に見てください。

積分の式の計算

それでは、積分の式を解いていきます。

まず積分の公式ですが、今回は下の公式を使用します。

$$\int \cos ax \, dx=\displaystyle\frac{1}{a} \sin ax + C$$

この公式を使用すると、次のように計算できます。

$$E=\displaystyle\frac{{V_ {peak}}^{2} }{2R} \left(\int_{0}^{T} \, dt -\int_{0}^{T} \cos 2\omega t \, dt \right)$$

$$=\displaystyle\frac{{V_ {peak}}^{2} }{2R} \left(\left[ t \right]_{0}^{T} -\left[\displaystyle\frac{1}{2\omega} \sin 2\omega t \right]_{0}^{T} \right)$$

$$=\displaystyle\frac{{V_ {peak}}^{2} }{2R} \left(\left(T-0\right) -\left(\displaystyle\frac{1}{2\omega} \sin 2\omega T - \displaystyle\frac{1}{2\omega} \sin 2\omega 0 \right) \right)$$

「$\omega=2\pi f$」なので、上の式は下のようになります。

$$E=\displaystyle\frac{{V_ {peak}}^{2} }{2R} \left(T -\displaystyle\frac{1}{2\omega} \left( \sin (2 ✕ 2 \pi f T) - \sin 0 \right) \right)$$

「$f$」は周波数、「$T$」は周期なので、「$ft=1$」になります。

具体的な数字で書くと50Hz（Hz=1/秒）✕0.02秒=1になります。

そうすると、上の式は下のようになります。

$$E=\displaystyle\frac{{V_ {peak}}^{2} }{2R} \left(T -\displaystyle\frac{1}{2\omega} \sin (2 ✕ 2 \pi ✕1) \right)$$

$$=\displaystyle\frac{{V_ {peak}}^{2} }{2R} \left(T -\displaystyle\frac{1}{2\omega} \sin 4 \pi \right)$$

$$=\displaystyle\frac{{V_ {peak}}^{2} }{2R} \left(T -\displaystyle\frac{1}{2\omega} ✕0 \right)$$

$$=\displaystyle\frac{{V_ {peak}}^{2} T }{2R} $$

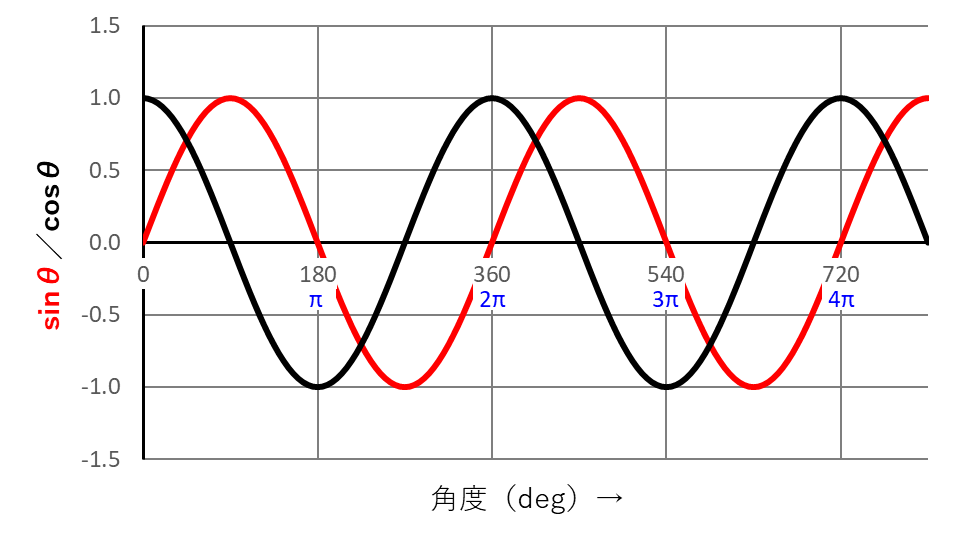
参考までに、「$\sin 0$」や「$\sin 4\pi$」は下のグラフの赤い線からゼロになることが分かると思います。