電気回路_コンデンサーのエネルギー〔５〕

2023年4月17日 2023年4月23日

講師Kazu

これまで、コンデンサーの容量値（キャパシタンス）や電荷量、エネルギーを求める計算式について書きましたが、今回は具体的な数値を使って計算してみます。

コンデンサーの容量値や電荷量、エネルギーの計算式だけでは、物理的なイメージがつかみづらいので、具体的な数字を入れて計算してみます。

今回はおおざっぱなイメージをつかむことが目的なので、計算結果は四捨五入で上位二桁に丸めるつもりです。

まずは、コンデンサーの容量値を計算で求めます。

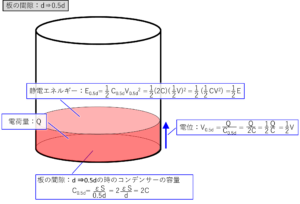
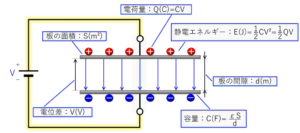
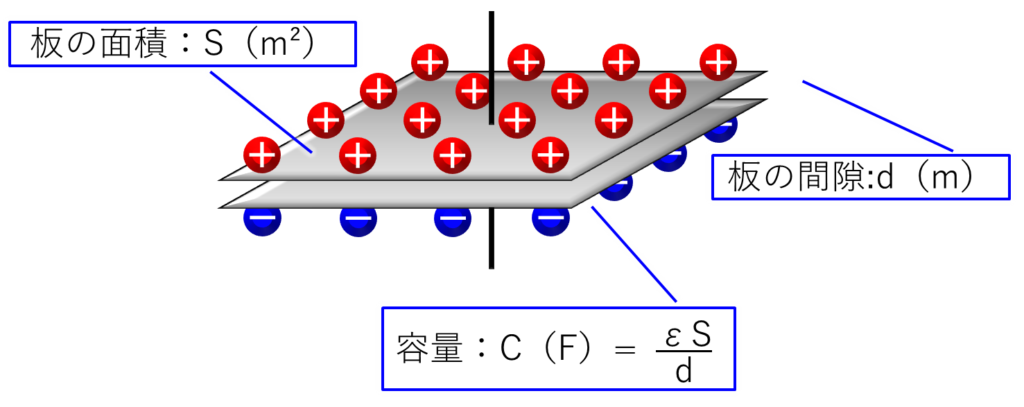
下の絵には、2枚の板を向かい合わせに置いた板の面積をＳ、板の間隔をｄとしたときのコンデンサーの容量値：Ｃを求める計算式を書いています。

今回のコンデンサーの構成は、1cm✕10cmの長方形に切ったアルミ箔を紙の上に置き、それをくるくる巻いて円筒状にしたイメージです。

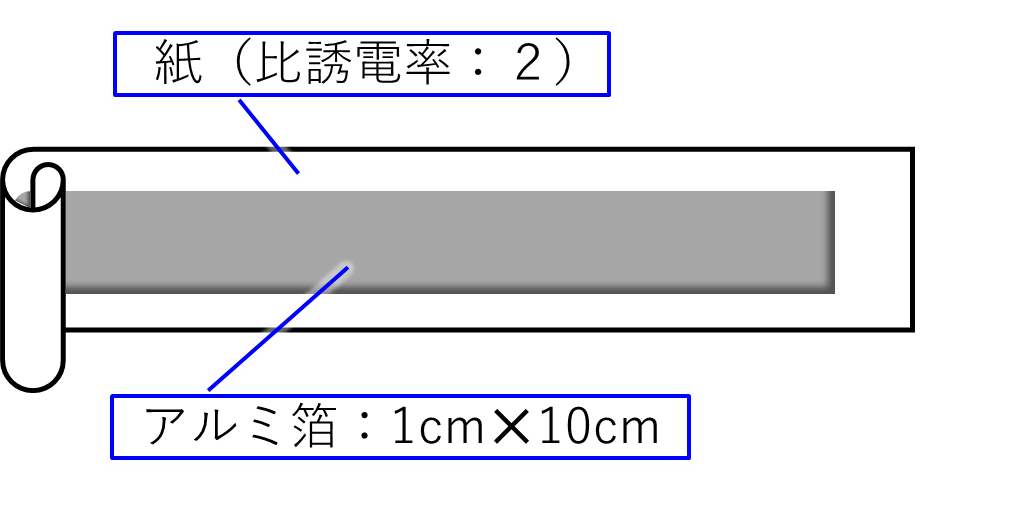
上の絵はアルミ箔と紙が一組ですが、これをもう一組用意して重ねることで、2枚の板を向かい合わせたのと同じ構成にします。

一般的な紙は、電気をほとんど通さない絶縁体に分類されるので、紙の両側に置いた2枚のアルミ箔に電荷を蓄えることができます。

紙を間に挟んで向かい合わせに置いたアルミ箔の面積は1cm✕10cmとしたので、単位をmにすると「$1✕10^{-2}m✕1✕10^{-1}m$」になります。

紙の厚さを0.1mm（⇒$1✕10^{-4}m$）、紙の比誘電率：$ε_r=2$として計算すると、このコンデンサ－の容量値は下のように計算できます。

$$C=\displaystyle\frac{εS}{d}=\displaystyle\frac{ε_0ε_rS}{d}$$

$$=\displaystyle\frac{(8.9✕10^{-12}✕2)✕(0.01✕0.1)}{0.0001}$$

$$=\displaystyle\frac{(8.9✕10^{-12}✕2)✕(1✕10^{-2}✕1✕10^{-1})}{1✕10^{-4}}$$

$$=(8.9✕2)\displaystyle\frac{(10^{-12}✕10^{-2}✕10^{-1})}{10^{-4}}$$

$$=17.8✕10^{(-12-2-1+4)}$$

$$=17.8✕10^{-11}$$

$$=178✕10^{-12}$$

$ε_0$は、前にも少し書きましたが真空中の誘電率（正確には電気定数というようです）で、その値は約$8.9✕10^{-12}$です。（単位は「F/m」⇒Fはファラッドで、mはメートル）

上の計算により、今回の紙とアルミ箔で作成したコンデンサーの容量値（キャパシタンス）は、約180pFになります。

「pF」の「p」は補助単位で「$10^{-12}$」を表して「ピコ」といいます。

「pF」の「F」は静電容量（コンデンサーの容量値、キャパシタンス）の単位で「ファラッド」です。

これまでも、ヘクトやキロなどを使ってきましたが、自分がよく見かける補助単位を下の表に書いておきます。

今回の「p：ピコ」は、この表では下から二つ目でかなり小さな数字を表すときに使用します。

余談ですが「キロ」から「ミリ」までの補助単位は、「キロキロとヘクトデカけたメートルが、デシに追われてセンチミリミリ」と覚えるんだと小学校か中学のときに教わりました。

ちなみに「メートル」は補助単位ではなく、長さや距離の単位なので上の表に書いていません。

今回の投稿は、コンデンサーの容量値だけになりましたが、次回も具体的な数値を使った計算を続けます。

よろしければ以下のバナーをクリックしていただけると励みになります！