コンデンサーに加えた交流電圧・電流〔２〕（交流の電流波形から電圧波形をイメージ）

前回は、コンデンサーに交流電流を加えたときの電圧波形を、計算式を使って求めましたが、今回はイメージで電流と電圧の波形を考えます。

想定する回路と電流波形

想定する回路は前回と同じで、周波数：50Hz、実効値：1Armsの交流電流源に、「50Hzで100Ωの抵抗値」になる「容量値：31.8μF」のコンデンサーを接続しています。

まず、回路図左側の電流源「\(I(t)=I_{peak} \sin (\omega t)\) 」の波形は下記になります。

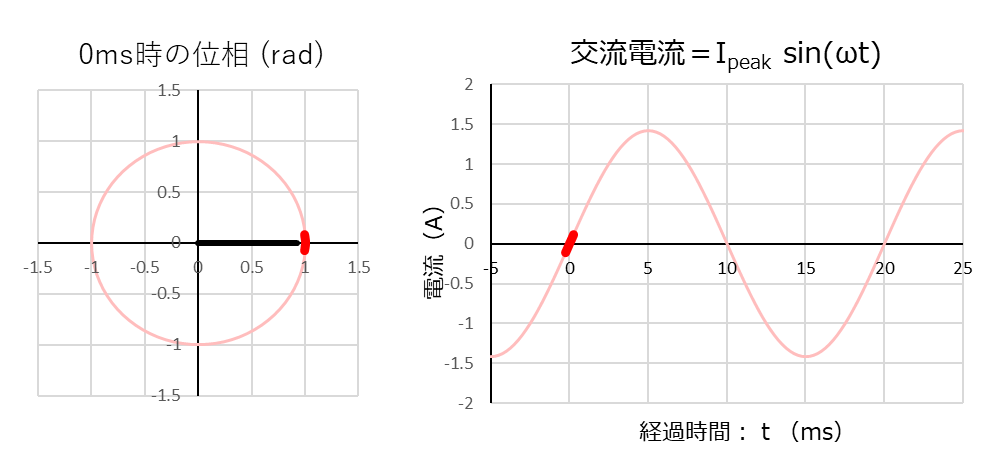
これは「Ipeak=1.41(A)」「ω=2πf=2π✕50=100π (rad/s) 」としたときのグラフです。

このとき、コンデンサーの両端に生じる電圧波形は下記です。

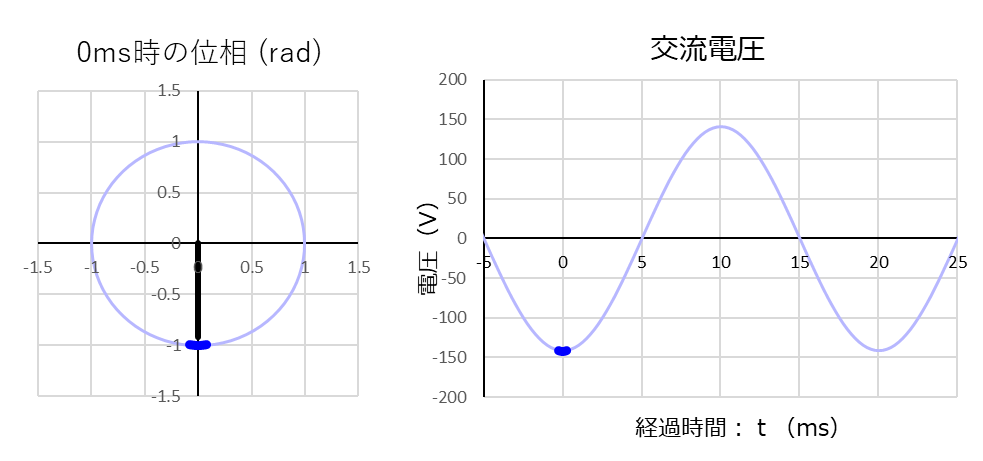
これらの波形を使い、まずは「経過時間：0ms」の波形から見ていきます。

経過時間：0ms

前の項と同じ波形を、もう一度貼りつけます。

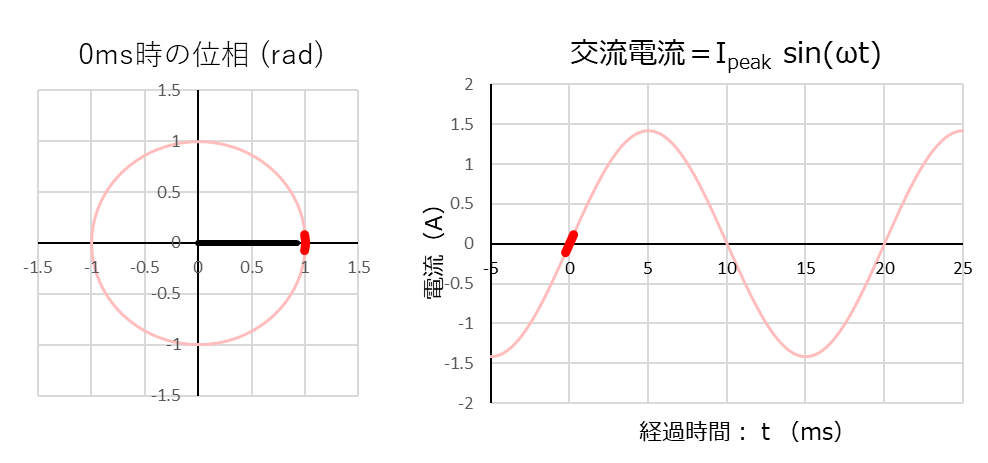
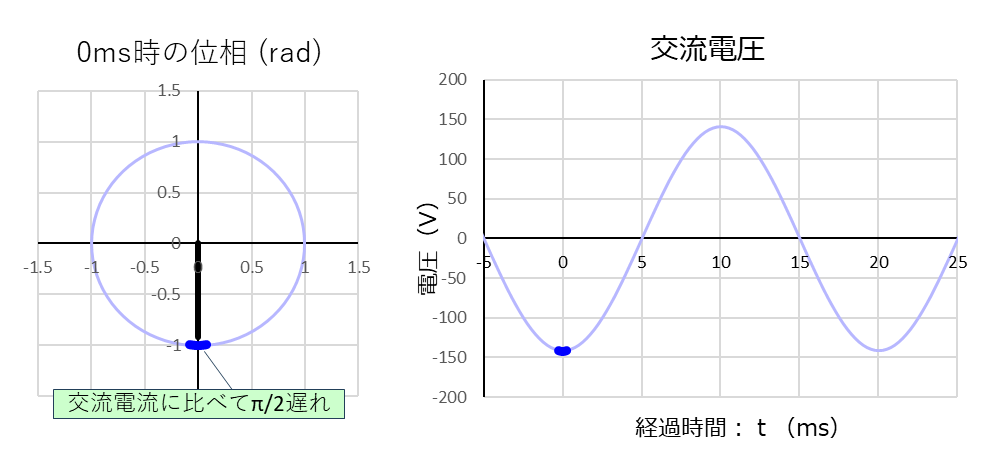
上側の赤い線のグラフが電流、下側の青い線のグラフが電圧の波形です。

「経過時間：0ms」での電流源の電流はほぼゼロなので、コンデンサーの電圧はあまり変わりません。

電流は「経過時間：0ms」をはさんでマイナスからプラスに変化しているので、電圧は降下から上昇に転じます。

過去の投稿「電気回路_コンデンサーの動作【直流】〔３〕」で書いた水槽のイメージのように、電流の流れる方向がプラスだと電位が上がり、マイナスだと電位が下がるイメージです。

その様子は太い赤線と、太い青線が示します。

また、「経過時間：0ms」時点での電流波形と電圧波形の位相を比べると、電流に対して電圧は「\(\displaystyle\frac{\pi}{2}(⇒90°)\)」遅れています。

経過時間：5ms

次に、5ms経過後の電流と電圧の波形です。

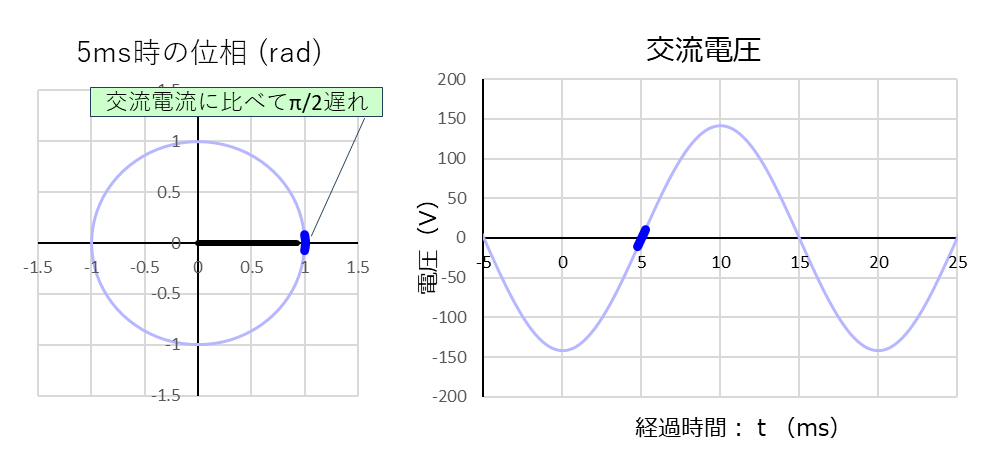
「経過時間：5ms」では、電流値が最大の1.41Aになるのでコンデンサーに流れ込む電流は最大となり、電圧は最大傾斜で上昇します。

その様子は、上のグラフの太い赤線と太い青線が示しています。

「経過時間：5ms」の電流波形と電圧波形の位相を比べると、電流に対して電圧はやはり「\(\displaystyle\frac{\pi}{2}(⇒90°)\)」遅れています。

経過時間：10ms

次は、10ms経過後の電流と電圧の波形です。

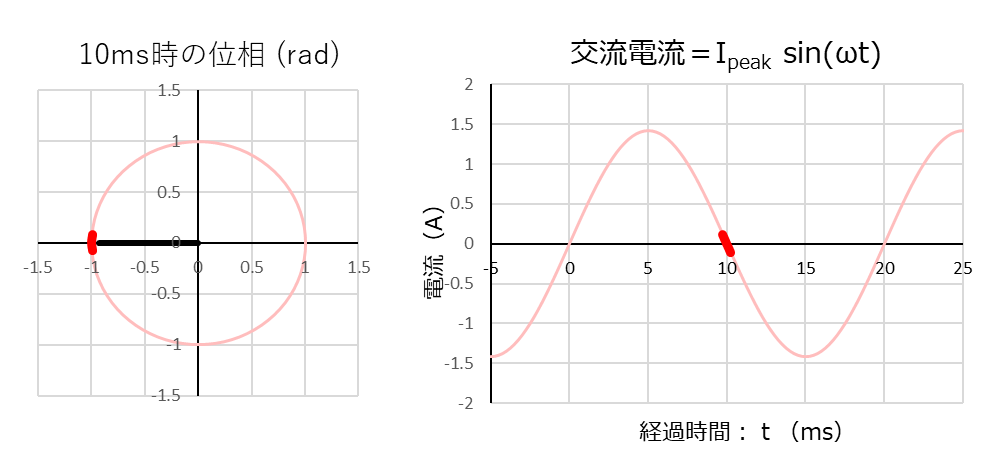
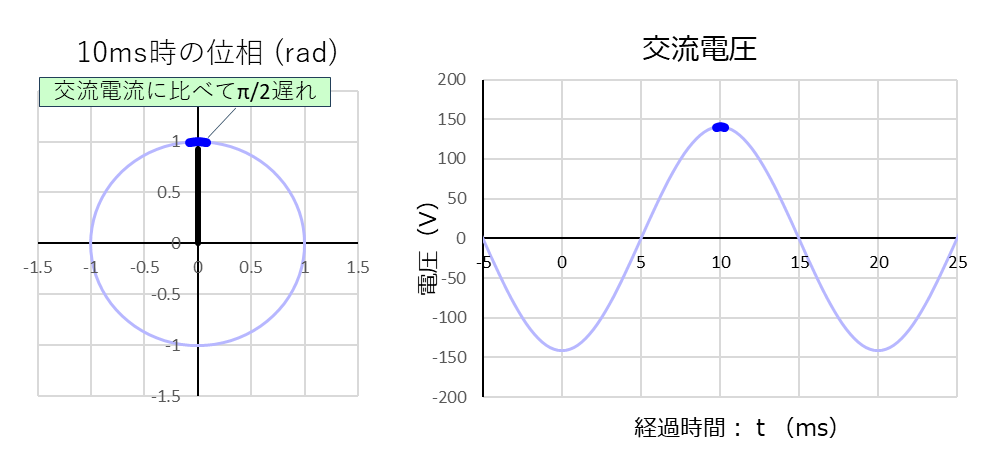
「経過時間：10ms」で、電流は再びほぼゼロになりますが、今回は電流がプラスからマイナスに変わります。

電流がほとんど流れないので、電圧はあまり変化しませんが、電圧は上昇から降下に転じます。

その様子は、上のグラフの太い赤線と太い青線になります。

「経過時間：10ms」の電流波形と電圧波形の位相を比べると、電流に対して電圧はやはり「\(\displaystyle\frac{\pi}{2}(⇒90°)\)」遅れます。

経過時間：15ms

最後は、15ms経過後の電流と電圧の波形です。

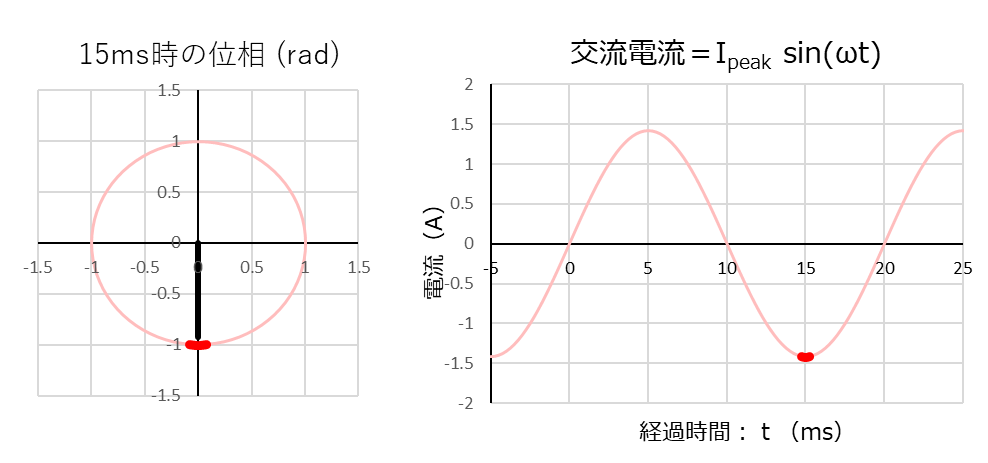
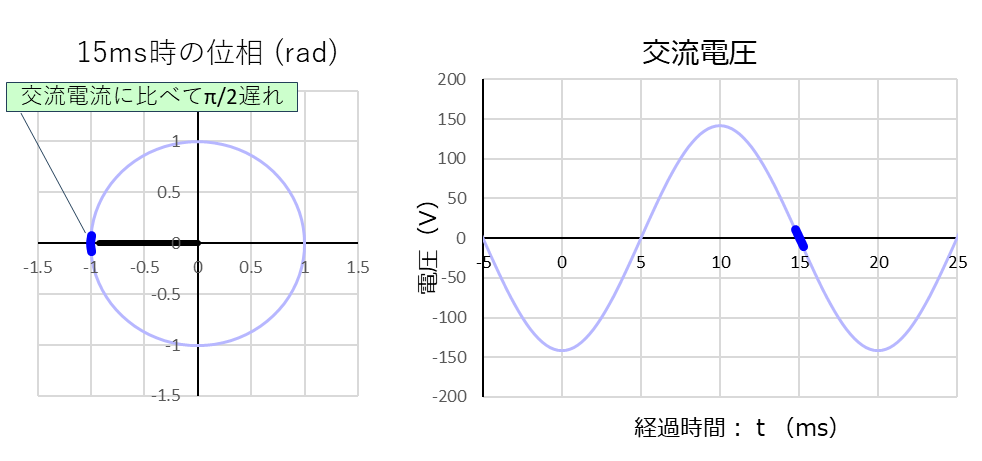
「経過時間：15ms」での電流値は最小の-1.41Aなので、コンデンサーから流れ出す電流は最大となり、電圧は最大傾斜で降下します。

その様子は、上のグラフの太い赤線と太い青線になります。

「経過時間：15ms」の電流波形と電圧波形の位相を比べると、ここでも電流に対して電圧はやはり「\(\displaystyle\frac{\pi}{2}(⇒90°)\)」遅れます。

まとめ

今回は、波形の周期：20msを4分割して、5msごとに電流と電圧の波形を確認しました。

今回の結果をまとめると、交流電流源にコンデンサーを接続したときに生じる電圧波形は、電流波形に対して常に「\(\displaystyle\frac{\pi}{2}(⇒90°)\)」遅れることが分かります。

この関係を計算式で求めることも大切ですが、波形をイメージできることも大切と自分は考えています。

次回は、電流源ではなく電圧源をコンデンサーに接続した場合について考えていこうと思います。

よろしければ以下のバナーをクリックしていただけると励みになります！

にほんブログ村
人気ブログランキング