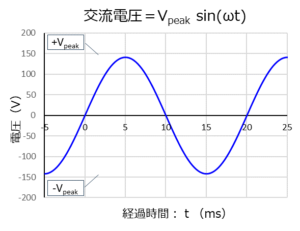
コンデンサーに加えた交流電圧・電流〔1〕(交流電流をコンデンサーに印加)
前回は、交流の電圧源や電流源に抵抗を接続して波形や位相を比較しましたが、今度はコンデンサーに接続します。
電流とコンデンサーと電圧の関係式
まずは、「電流源」に接続した「抵抗」「コイル」「コンデンサー」に生じる電圧を表す式を下に示します。
$$V(t)=L\displaystyle\frac{dI(t)}{dt}+RI(t)+\displaystyle\frac{1}{C}\int I(t)dt$$
この式は、ウィキペディアの「リアクタンス」に書かれていましたが、同様の式は過去の投稿「電気回路_コイルの動作【直流】〔3〕」にも書いています。
今回は「コンデンサー」なので、下の式だけを使います。
$$V(t)=\displaystyle\frac{1}{C}\int I(t)dt$$
想定する回路図は下記になります。
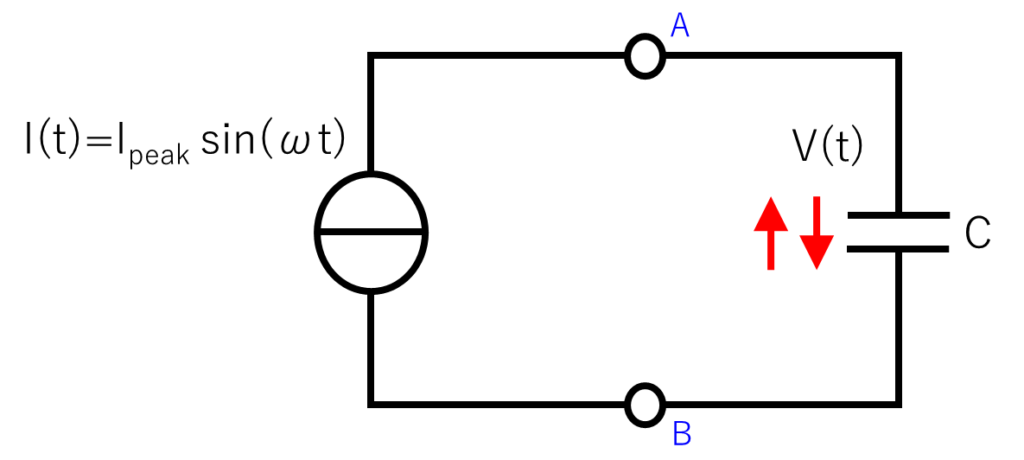
これまで、交流の電圧源や電流源には「\(V_{AC}(t)\) 」や「\(I_{AC}(t)\) 」を使っていましたが、ここで使用するのは交流だけなので「\(_{AC}\) 」は省きました。
電流の変化から電圧の変化を計算する式を求める
「コンデンサー:\(C\)」に、左の交流電流源「\(I(t)=I_{peak}\sin(\omega t)\)」を接続したときに、「コンデンサー:\(C\)」の両端に表れる「電圧:\(V(t)\)」を、まずは計算で求めます。
上の式に「\(I(t)=I_{peak}\sin(\omega t)\)」を入れると下記になります。
$$V(t)=\displaystyle\frac{1}{C}\int I_{peak}\sin(\omega t) dt$$
「\(I_{peak}\)」は「経過時間:t」が変わっても変化しないので、積分の前に出します。
$$V(t)=\displaystyle\frac{I_{peak}}{C}\int \sin(\omega t) dt$$
この式を解くために、下の三角関数の積分の公式を使います。
$$\int \sin ax dx=-\displaystyle\frac{\cos ax}{a} +A$$
上の式の右端の「\(A\) 」は定数で、通常は「\(C\) 」を使いますが、コンデンサーの「容量値」に「\(C\) 」を使っているので「\(A\) 」を使いました。
積分の公式に使われる「\(C\) 」は定数なので、おそらく英語で定数を表す「constant」からきていると思います。
ただ今回は、定数「\(A(C)\) 」は無視して下の積分の公式で話を進めます。
$$\int \sin ax dx=-\displaystyle\frac{\cos ax}{a}$$
この公式を使って積分の式を解いていくと下記になります。
$$V(t)=\displaystyle\frac{I_{peak}}{C}✕ \int \sin(\omega t) dt$$
$$V(t)=\displaystyle\frac{I_{peak}}{C}✕ \left(-\displaystyle\frac{\cos(\omega t)}{\omega}\right)$$
$$V(t)=-\displaystyle\frac{I_{peak}}{\omega C} \cos(\omega t)$$
この式と、抵抗の式「\(V(t)=RI_{peak}\sin(\omega t)\) 」を見比べると、「\(R\) 」に相当するのが「\(\displaystyle\frac{1}{\omega C}\) 」であることが分かります。
ちなみに「プラスとマイナス」、「\(\sin\)と\(\cos\) 」の違いは位相に関係します。
計算式に具体的な数値を入れてグラフを作成
ここからは、具体的な数字を入れていきます。
「抵抗」のときと同じように、電流値は「電流の実効値:\(I=1A_{rms}\) 」⇒「\(I_{peak}=1\sqrt2 A \) 」を使用します。
前の項で、「\(R\)」に相当するのが「\(\displaystyle\frac{1}{\omega C} \) 」と書きましたが、「\(\displaystyle\frac{1}{\omega C} \) 」の値は「周波数:\(f=50Hz\)」で「\(R=100Ω\)」に相当する値とします。
この「\(R=100Ω\)」は、抵抗の投稿で使用した抵抗値と同じにしました。
「周波数:\(f=50Hz\)」で、「抵抗値:\(R=100Ω\)」相当になる「コンデンサーの容量値:\(C\)」は下のように計算できます。
$$\displaystyle\frac{1}{\omega C}=R=100$$
$$\displaystyle\frac{1}{2\pi f C}=100$$
$$\displaystyle\frac{1}{2\pi 50 C}=100$$
$$\displaystyle\frac{1}{100\pi C}=100$$
$$\displaystyle\frac{1}{100\pi}✕\displaystyle\frac{1}{100}=C$$
$$C=\displaystyle\frac{1}{10000\pi}$$
$$C=31.8✕10^{-6}$$
$$C=31.8μF$$
コンデンサーの値は\(31.8μF\) (マイクロファラッド)になりました。
それでは、この条件で\(V(t)\)を計算します。
$$V(t)=-\displaystyle\frac{I_{peak}}{\omega C} \cos(\omega t)$$
$$V(t)=-I_{peak}✕\displaystyle\frac{1}{\omega C}✕ \cos(2 \pi f t)$$
$$V(t)=-1\sqrt2✕100✕ \cos(2 \pi 50 t)$$
$$V(t)=-100\sqrt2 \cos(100 \pi t)$$
$$V(t)≒-141 \cos(100 \pi t)$$
「電流:\(I(t)\) 」の式にも具体的な数字を入れると下記になります。
$$I(t)=I_{peak}\sin(\omega t)$$
$$I(t)=\sqrt2 \sin(2\pi f t)$$
$$I(t)≒1.41 \sin(100\pi t)$$
これらの式をグラフ化します。
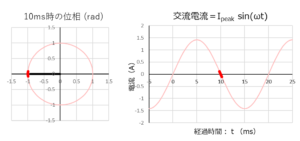
まずは、「経過時間:-5~25ms」で「電流:\(I(t)\) 」をグラフ化します。

「抵抗」のときと同様、右のグラフは横軸が経過時間で、縦軸が電流値です。
左の単位円のグラフには、「経過時間:0ms」時の位相(角度)を太い赤と黒の線で示します。
同様に「経過時間:-5~25ms」で「電圧:\(V(t)\) 」をグラフ化します。
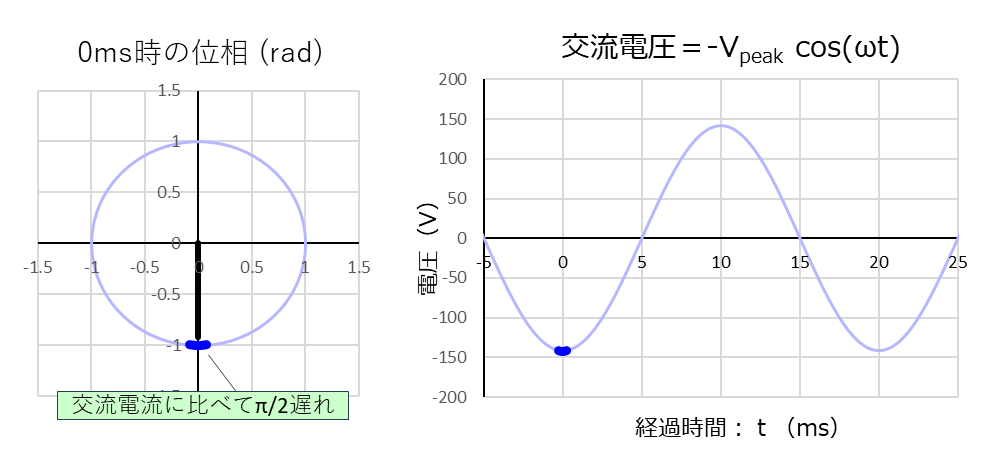
左の単位円のグラフを見ると、「経過時間:0ms」時の位相が真下になっています。
単位円のグラフは、時間の経過とともに反時計回りに回転するので、電流に比べると電圧の位相が「\(\displaystyle\frac{\pi}{2}(rad)=90(deg)\)」遅れていることが分かります。
次回は、この「電流」と「電圧」の関係を波形イメージで説明していこうと思います。
よろしければ以下のバナーをクリックしていただけると励みになります!
にほんブログ村
人気ブログランキング