電気回路_コンデンサーのエネルギー〔７〕

前回に続き、アルミ箔と紙で作ったコンデンサーに電圧を加えたときに、コンデンサーに蓄えられる電荷量や静電エネルギーを求めます。

コンデンサーに6Vの電池を接続

前回はコンデンサーに3Vの電池を接続しましたが、今回は6Vの電池を接続します。

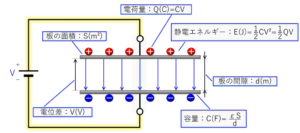
下の画像は、前回と同じ画像です。

コンデンサーの容量値は、前回、前々回計算した\(178pF\)です。

前回と同じように、電池が6Vの時の電荷量：\(Q_{6V}\)と、静電エネルギー：\(E_{6V}\)を計算します。

$$Q_{6V}=CV=178✕10^{-12}✕6=1068✕10^{-12}(C)$$

\(Q_{6V}\)は\(1068pC\)になりました。

次に静電エネルギー：\(E_{6V}\)を計算します。

$$E_{6V}=\displaystyle\frac{1}{2}CV^2(J)$$

$$E_{6V}=\displaystyle\frac{1}{2}✕178✕10^{-12}✕6^2(J)$$

$$E_{6V}=3204✕10^{-12}(J)$$

\(3204✕10^{-12}(J)\)は、補助単位を使って表すと\(3204pJ\)や\(3.204nJ\)になります。

前回の電池の電圧が3Vのときの電荷量、静電エネルギーと比較すると下の表になります。

コンデンサーの電圧が2倍になると、電荷量は電圧に比例して2倍になりますが、静電エネルギーは2の二乗に比例して4倍になります。

これは、計算式を見ると分かりますが、〔４〕で使用した下の画像からもイメージできると思います。

円柱の水槽に水を入れたイメージと同じように、円柱をイメージしたコンデンサーに電荷が蓄えられたイメージ図です。

水位に相当する電位と、水量に相当する電荷量は比例関係にあります。

それに対して静電エネルギーは、電位が低い位置と高い位置では、同じ電荷量でも同じ静電エネルギーではありません。

このことは、〔４〕の投稿を見ていただければイメージしていただけると思います。

電位が高くなると、電荷量が比例して増えますが、同じ電荷量でも電位に比例して静電エネルギーが増えるので、結果的に電位の二乗に比例して静電エネルギーが増えていきます。

位置エネルギーと静電エネルギー

最後に、位置エネルギーの計算式に使用されている「質量」「重力加速度」「高さ」が、静電エネルギーの計算式では何に相当するのかを書きます。

ここでの位置エネルギーは、水槽に貯めた水の位置エネルギーではなく、例えば高さ1mの位置に1kgの重りを置いたときの重りの位置エネルギーです。

位置エネルギーと静電エネルギーの計算式を下に示しますが、ここではエネルギーを示す記号として「W（仕事）」を使用します。

エネルギーも仕事も、単位はジュール（J）で同じものです。

このあと、「E」は別の記号として使用します。

それでは、まず位置エネルギーの計算式です。

$$W=mgh$$

一応、記号の説明も書いておきます。

W(J)：仕事・エネルギー（ジュール）

m(kg)：質量

g(m/s²)：重力加速度

h(m)：高さ

次に静電エネルギーの計算式です。

$$W=QV$$

Q(C)：電荷量（クーロン）

V(V)：電位（ボルト）

このままだと、何が何に相当するのかが分からないと思います。

静電エネルギーの式を少し変形してみます。

電圧：V（V）は、電界の強さ：E（V/m）に距離：d（m）をかけると求まるので、下のように変形できます。

$$W=QV=QEd$$

「位置エネルギーの定義」は「１ニュートンの力がその力の方向に物体を１メートル動かすときの仕事」なので、「位置エネルギー」＝「力」✕「距離」になります。

位置エネルギーでは「力」＝「質量」✕「重力加速度」です。

静電エネルギーでは「力」＝「電荷量」✕「電界の強さ」です。

例えば、質量：1kgの物体を重力加速度：9.8m/s²の地上で手のひらの上に置くと、手のひらには9.8N（ニュートン）の力が加わります。

同様に、電荷量：1Cの電荷を帯びた物体を電界の強さ：1V/mの場所に置くと、その物体には1N（ニュートン）の力が加わります。

日常生活でこの力を感じることは少ないかもしれませんが、静電気を帯びた下敷きに髪の毛が引っ張られたり、乾燥しているときに衣類が体にまとわりついたりするときの力と原理的には同じです。

このことから、位置エネルギーと静電エネルギーの計算式で、何が何に相当するかと考えると下記のようになります。

自分の静電エネルギーのイメージですが、「電界の強さ」が斜面の傾斜で、その斜面を「電荷」という球状の重りを「電界の強さ」に逆らって押し上げていくと、その重りの電位が上昇するので、位置エネルギーと同じように静電エネルギーが増えていくという感じです。

これは自分のイメージなので、表現としては厳密でない点はあると思います。

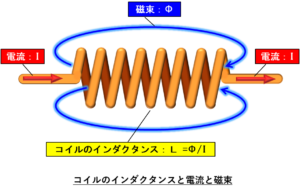
さて、コンデンサーの話は今回で一度終了して、そろそろコイルの話を少し書こうと思います。

よろしければ以下のバナーをクリックしていただけると励みになります！

にほんブログ村