電気回路_コンデンサーのエネルギー〔３〕

今回はコンデンサーの中の電界強度の話を中心に書いてみようと思います。

コンデンサーの中の電界強度のおさらいと説明

前回もコンデンサーの中の電界強度（電界の強さ）について書きましたが、

下のような絵を使用しました。

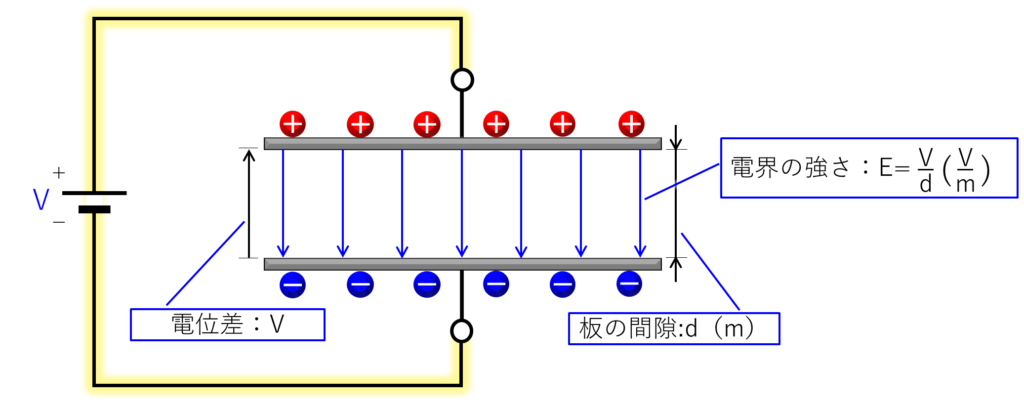
前回との違いは、2枚の板に定電圧源（電池）の回路を描き足した点です。

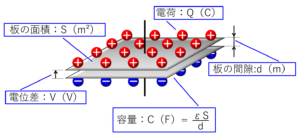
2枚の板の間に「V」の電位差を与えると、コンデンサーには電荷「Q」が蓄えられます。

この電荷「Q」の値は、下の式で求めることができます。

$$Q=CV$$

これまでもコンデンサーの容量値として「C」を何度か使用してきたと思いますが、「C」は下記の式で求めることができます。

$$C=\displaystyle\frac{εS}{d}$$

前回、下の絵は貼り付けただけであまり説明しませんでしたが、下の絵に描いているように「S」は板の面積です。

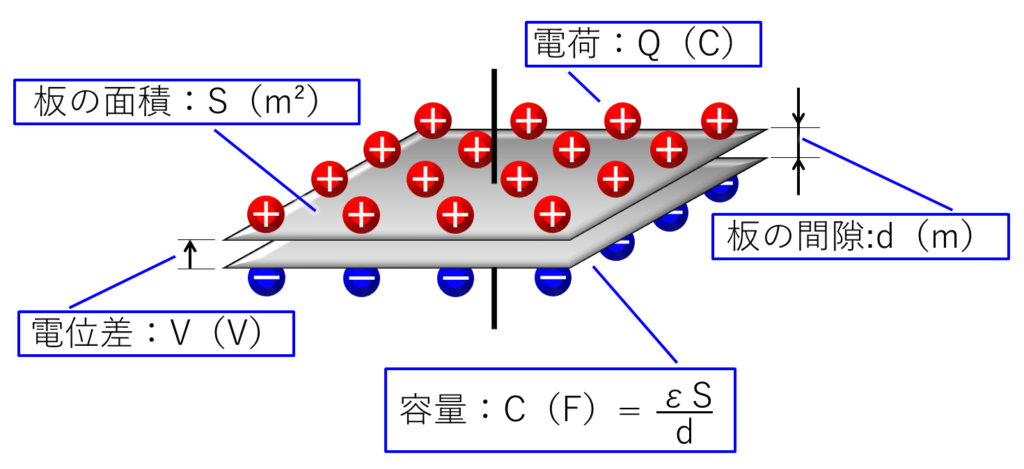
「ε」は板の間に入っている物質の「誘電率」です。

物理学的に厳密な「誘電率」の説明は自分には無理ですが、もう少し踏み込むと「ε」は下のように分解されます。

$$ε=ε_rε_0$$

「\(ε_0\)」は「真空中の誘電率」で、おそらく厳密には「電気定数」とよばれています。

この「真空中の誘電率：\(ε_0\)」に対して、例えば水＠20℃の誘電率は約80倍なので、「水の比誘電率：\(ε_r\)」は約80となります。

ちなみに「空気の比誘電率：\(ε_r\)」は1.00059なので、空気の誘電率は真空とほぼ同じです。

「真空中の誘電率：\(ε_0\)」の具体的な値は約「\(8.854×10^{-12} \)」で、単位は\((F/m)\)です。

\((F/m)\)の\((F)\)はコンデンサーの容量の単位で「ファラッド」、\((m)\)は長さの単位で「メートル」です。

先ほどの式を、自分は下の式のイメージで理解しています。

$$C=\displaystyle\frac{εS}{d}=\displaystyle\frac{S}{\left(\displaystyle\frac{d}{ε}\right)}=\displaystyle\frac{S}{\left(\displaystyle\frac{d}{ε_rε_0}\right)}=\displaystyle\frac{S}{\displaystyle\frac{1}{ε_r}\left(\displaystyle\frac{d}{ε_0}\right)}$$

この式のイメージは、2枚の板の間の誘電率が大きくなると、2枚の板の間の距離が縮まるイメージです。

例えば、コンデンサーを構成する2枚の板を空気中に8mm離して置いていたとして、その2枚の板をそのまま水の中に入れると板の間隔が1/80の0.1mmに近づいたのと同じ効果があり、容量値は80倍に増えます。

さて、ここからは電界の話を書こうと思います。

2枚の板の間隔と電界強度の関係

まずは、先ほどの絵を再度貼り付けます。

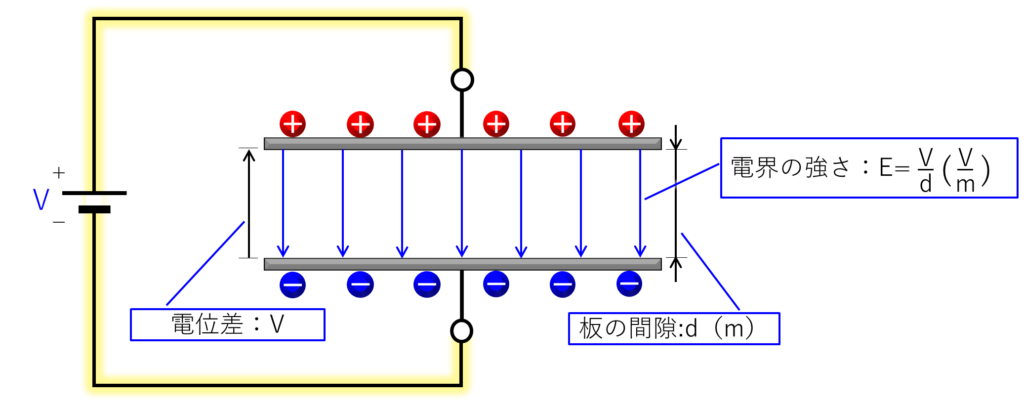
このコンデンサーから定電圧源（電池）を取り外すと下記になります。

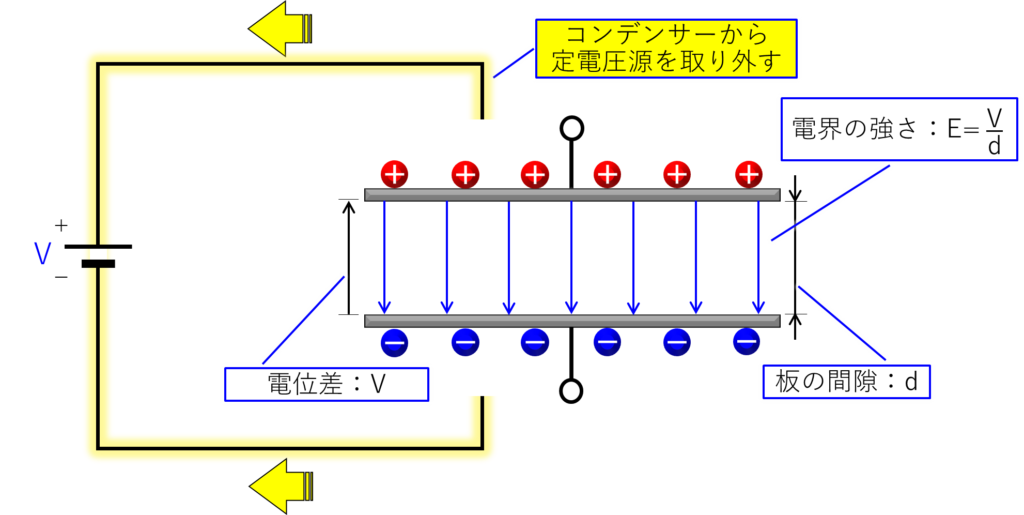
このコンデンサだけを取り出すと下記になります。

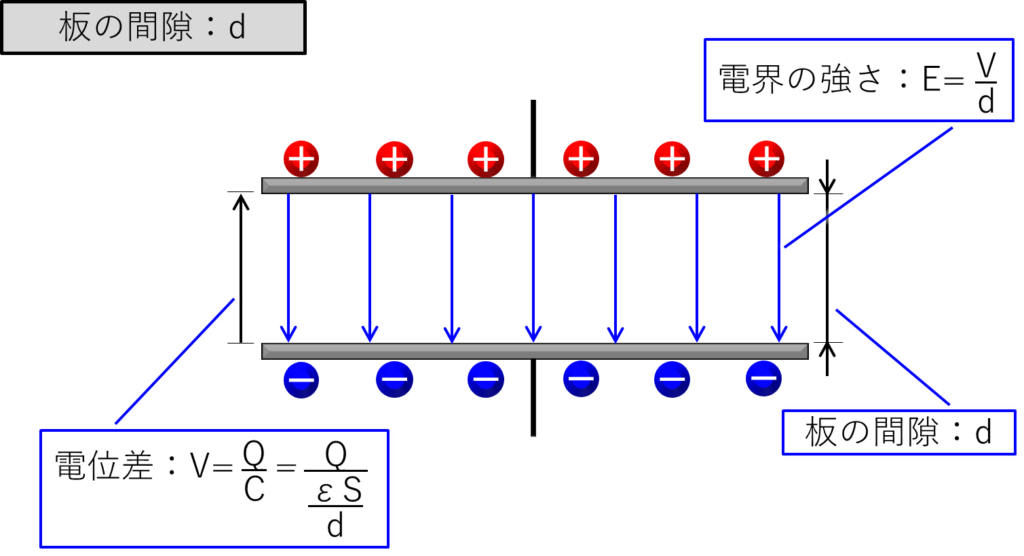
前の項でも書いたように、板の間隙が「d」の場合の電位差は「V」で電界の強さは「\(\displaystyle\frac{V}{d}\)」となります。

次に、そのままの状態で2枚の板の間隙を2倍の「2d」に広げると下の絵のようになります。

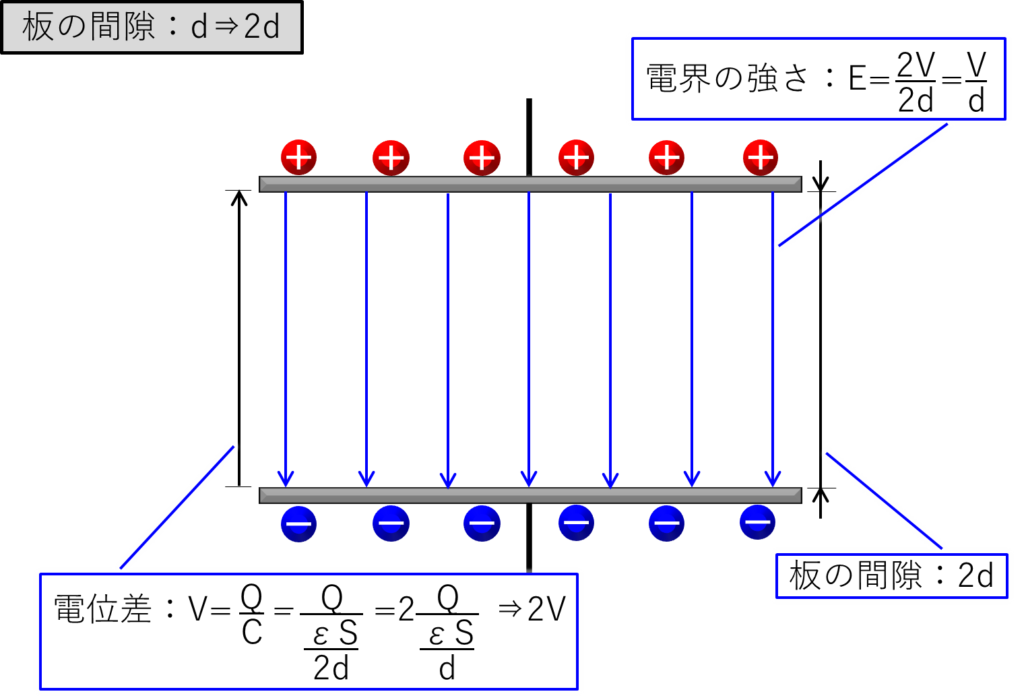
板の間隙が2倍の「2d」になると、電位差は上の絵に書いたように容量値：Cが半分になるので「2V」になります。

そうすると、電界の強さは「\(\displaystyle\frac{2V}{2d}=\displaystyle\frac{V}{d}\)」となり、板の間隙が「d」のときと同じです。

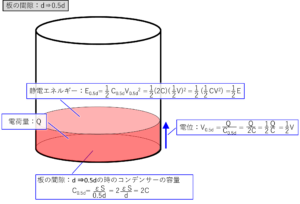
今度は、2枚の板の間隙を半分の「0.5d」にした絵を下に示します。

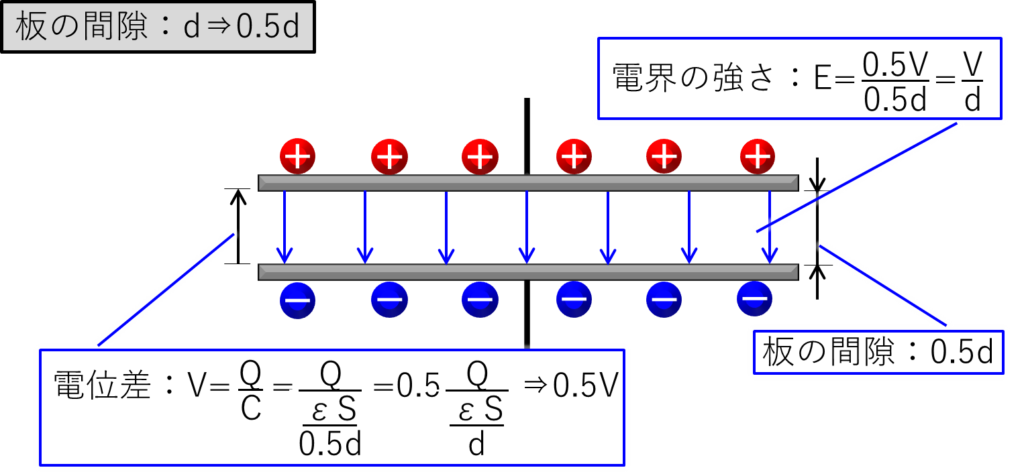
板の間隙が半分の「0.5d」になると、電位差は上の絵に書いたように容量値：Cが2倍になるので「0.5V」になります。

そうすると、電界の強さは「\(\displaystyle\frac{0.5V}{0.5d}=\displaystyle\frac{V}{d}\)」となり、板の間隙はやはり「d」のときと同じです。

最後に、2枚の板の間隙をn倍の「nd」にした絵を下に示します。

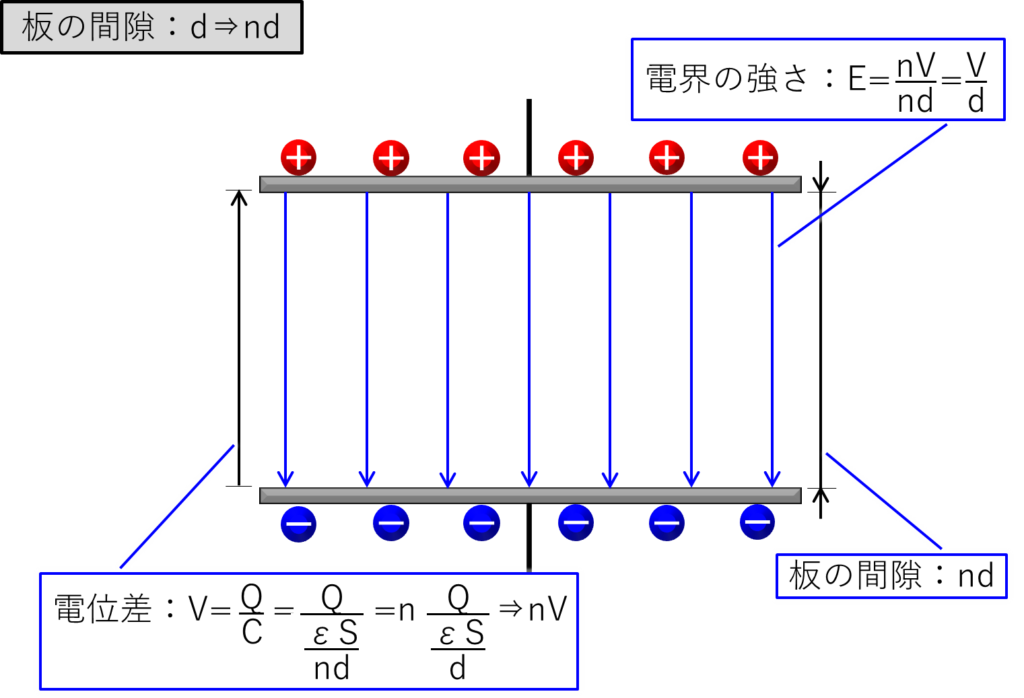
板の間隙をn倍の「nd」にすると、電位差は上の絵に書いたように容量値：Cが\(\displaystyle\frac{1}{n}\)倍になるので「nV」になります。

そうすると、電界の強さは「\(\displaystyle\frac{nV}{nd}=\displaystyle\frac{V}{d}\)」となり、板の間隙が「d」のときと同じです。

この結果から、2枚の板に蓄えた電荷の量が一定なら、板の間隔が広がっても狭くなっても、2枚の板の間の電界の強さは変わらないことになります。

時間が無くなったので、このときの2枚の板の静電エネルギーについては次回書きます。

よろしければ以下のバナーをクリックしていただけると励みになります！

にほんブログ村