コンデンサーに加えた交流電圧、電流〔３〕（交流電圧をコンデンサーに印加）

前回と前々回は、コンデンサーに交流の電流源を接続しましたが、今回は交流の電圧源を接続します。

想定する回路と関係式

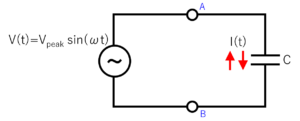
想定する回路は下記になります。

また、使用する関係式は「コンデンサーに加えた交流電圧・電流〔１〕」でも使用した下の式になります。

$$V(t)=\displaystyle\frac{1}{C}\int I(t)dt$$

この式の両辺を「時間：\(t\) 」で微分して、電流から電圧を求める式にしていきます。

電圧の変化から電流の変化を計算する式を求める

それでは、さっそく前の項の式を両辺を「時間：\(t\) 」で微分して解いていきます。

$$V(t)=\displaystyle\frac{1}{C}\int I(t)dt$$

$$\displaystyle\frac{dV(t)}{dt}=\displaystyle\frac{1}{C} I(t)$$

$$C \displaystyle\frac{dV(t)}{dt}=I(t)$$

$$I(t)=C \displaystyle\frac{dV(t)}{dt}$$

上の式に「\(V(t)=V_{peak}\sin(\omega t)\)」を入れて計算していきます。

$$I(t)=C \displaystyle\frac{dV(t)}{dt}$$

$$I(t)=C \displaystyle\frac{d(V_{peak}\sin(\omega t))}{dt}$$

$$I(t)=CV_{peak} \displaystyle\frac{d(\sin(\omega t))}{dt}$$

ここで、微分の公式を使います。

「\(\sin (\omega t) \) 」を「時間：\(t\) 」で微分すると「\(\omega \cos (\omega t) \) 」になります。

余談ですが、「\(\cos (\omega t) \) 」を「時間：\(t\) 」で微分すると「\(-\omega \sin (\omega t) \) 」になります。

「\(\sin\) 」や「\(\cos\) 」の前に「\(\omega\) 」が出るのは、「\(\omega t\) 」を「時間：\(t\) 」で微分した結果の「\(\omega\) 」が「\(\sin\) 」や「\(\cos\) 」の外に出るためです。

この説明だけだと分かりづらいので、ネットで微分の公式を調べてみてください。

それでは、上の式を微分します。

$$I(t)=CV_{peak} \displaystyle\frac{d(\sin(\omega t))}{dt}$$

$$I(t)=\omega CV_{peak} \cos(\omega t) $$

この式は、下の式に変形した方が電圧と電流の関係をイメージしやすいかもしれません。

$$I(t)=\displaystyle\frac{V_{peak}} {\displaystyle\frac{1} {\omega C}} \cos (\omega t) $$

この形にすると、「コンデンサーに加えた交流電圧・電流〔１〕」で書いたように、抵抗「\(R\) 」に相当するのが「\(\displaystyle\frac{1} {\omega C} \) 」になることが分かりやすいと思います。

計算式に具体的な数値を入れてグラフを作成

ここからは、計算式に具体的な数字を入れて計算し、それをグラフにしていきます。

今回も「抵抗」のときと同様、「電圧の実効値：\(V=100V_{rms}\) 」⇒「\(V_{peak}=100\sqrt2 V\) 」とします。

また「\(\displaystyle\frac{1} {\omega C} \) 」は、「コンデンサーに加えた交流電圧・電流〔１〕」と同じ「\(f=50Hz\) 」「\(C=31.8μF=31.8✕10^ {-6}F \) 」とすると下記になります。

$$\displaystyle\frac{1} {\omega C}=\displaystyle\frac{1} {2\pi f C} $$

$$=\displaystyle\frac{1} {2\pi✕50✕31.8✕10^{-6}} $$

$$=100(Ω)$$

この値を使うと、前の項の式は下記になります。

$$I(t)=\displaystyle\frac{V_{peak}} {\displaystyle\frac{1} {\omega C}} \cos (\omega t) $$

$$=\displaystyle\frac{100\sqrt2} {100} \cos (2 \pi f t) $$

$$=\sqrt2 \cos (2 \pi 50 t) $$

$$=\sqrt2 \cos (100 \pi t) $$

前後しますが、「電圧：\(V(t)\) 」の式にも具体的な数字を入れます。

$$V(t)=V_{peak}\sin (\omega t) $$

$$=100\sqrt2\sin (2\pi f t) $$

$$=100\sqrt2\sin (2\pi 50 t) $$

$$=100\sqrt2\sin (100\pi t) $$

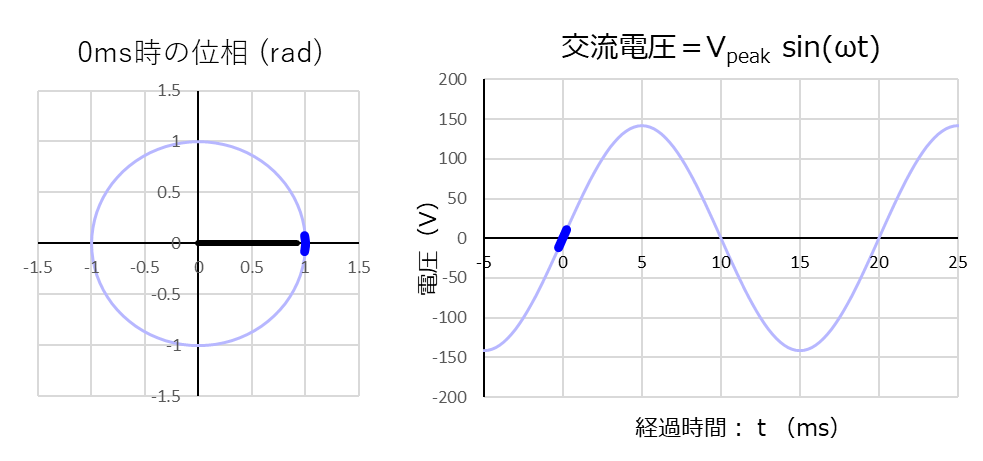
それでは「電圧：\(V(t)\) 」と「電流：\( I(t)\) 」をグラフ化します。

最初に「電圧：\(V(t)=100\sqrt2\sin (100\pi t) \) 」のグラフです。

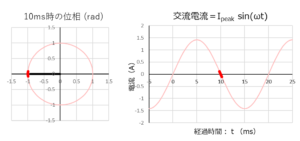
次に「電流：\(I(t)=\sqrt2 \cos (100 \pi t) \) 」のグラフです。

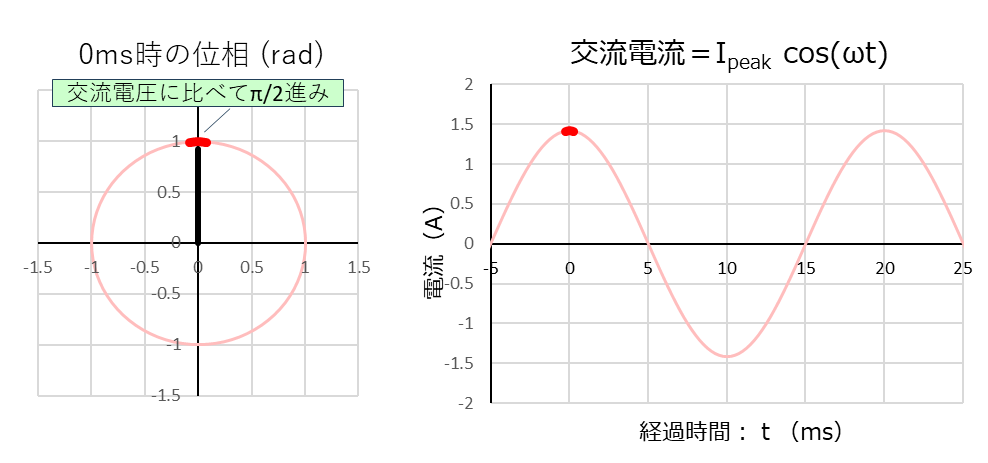
上下二つのグラフを見比べると、「経過時間：0ms」時の電流の位相が、電圧に比べて「\(\displaystyle\frac{\pi}{2} (rad)=90(deg)\) 」進んでいることが分かります。

次回は電流源のときと同じように、電圧源を接続したコンデンサーの「電圧」と「電流」の関係を、イメージを使って説明していきます。

よろしければ以下のバナーをクリックしていただけると励みになります！

にほんブログ村
人気ブログランキング