電気回路_コンデンサーのエネルギー〔６〕

前回はアルミ箔と紙で作ったコンデンサーの容量値を計算したので、今回はそのコンデンサーに電圧を加えてみます。

コンデンサー関連の計算式をおさらい

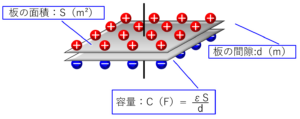
下の図に、電池の電圧をV(V)、コンデンサーの板の面積をS(m²)、板の間隔をd(m)、2枚の板の間に入れた紙の誘電率をε(F/m)としたときの容量値：C(F)、電荷量：Q(C)、静電エネルギー：E(J)を求める計算式を書きました。

繰り返しになりますが、単位の説明を書いておきます。

・電圧の単位：V（ボルト）

・面積の単位：m²（平方メートル）

・間隔の単位：m（メートル）

・誘電率の単位：F/m（ファラッド＿パー＿メートル）

・容量値の単位：F（ファラッド）

・電荷量の単位：C（クーロン）

・静電エネルギーの単位：J（ジュール）

それでは、コンデンサーの電荷量と静電エネルギーを計算していきます。

コンデンサーに3Vの電池を接続

まずは、前回の〔５〕で容量値を算出したコンデンサーに3Vの電池をつなぎます。

前回の容量値は次の条件で計算しました。

板の面積は、\(1(cm)✕10(cm)\)としたので\(0.01(m)✕0.1(m)=1✕10^{-3}(m^2)\)です。

2枚の板の間に厚さ\(0.1(mm)\)の紙を挟んだとしたので、間隔は\(0.1(mm)\)で\(1✕10^{-4}(m)\)です。

2枚の板の間に挟んだ紙の誘電率：\(ε\)は、紙の比誘電率：\(ε_r\)を\(2\)としました。

$$ε=ε_0✕ε_r=8.9✕10^{-12}(F/m)✕2=17.8✕10^{-12}(F/m)$$

\(ε_0\)は真空の誘電率（電気定数）です。

そうすると、このコンデンサーの容量値は下記になります。

$$C=\displaystyle\frac{εS}{d}(F)$$

$$=\displaystyle\frac{(17.8✕10^{-12})✕(1✕10^{-3})}{1✕10^{-4}}(F)$$

$$=17.8✕10^{(-12-3+4)}(F)$$

$$=17.8✕10^{-11}(F)$$

$$=178✕10^{-12}(F)$$

前回の投稿で書いたように、このコンデンサーの容量値は\(178pF\)です。

先ほどの画像を再掲載しましたが、このコンデンサーに\(3V\)の電池を接続したとき、コンデンサーに蓄えられる電荷量：\(Q_{3V}\)を計算します。

$$Q_{3V}=CV=178✕10^{-12}✕3=534✕10^{-12}(C)$$

\(Q_{3V}\)は\(534pC\)になりました。

\(534pC\)がどのくらいの電荷量かというと、電子1個の電荷量（電気素量）：\(e\)は\(1.6✕10^{-19}(C)\)なので、コンデンサーに蓄えられた電子の個数は下の式で計算できます。

$$電子の個数=\displaystyle\frac{Q_{3V}}{e}$$

$$=\displaystyle\frac{534✕10^{-12}}{1.6✕10^{-19}}$$

$$\simeq3.3✕10^9$$

計算した結果は\(3.3✕10^9\)なので、\(33\)億個になります。

コンデンサーに電池をつないだとき、コンデンサーに\(1A\)(アンペア)の電流が流れたと想定して、\(33\)億個の電子がコンデンサーに流れる時間を計算します。

まず、電流と電荷量の関係ですが、\(1\)秒間に\(1C\)(クーロン)の電荷が流れたときの電流が\(1A\)(アンペア)なので、電流を\(I(A)\)、電荷量を\(Q(C)\)、時間を\(t(s)\)とすると下の式になります。（※「\(s\)」は時間の単位で秒です。）

$$I=\displaystyle\frac{Q}{t}(A)$$

この式を「\(t\)=」に変形して、\(33\)億個の電子が流れる時間を計算します。

$$t=\displaystyle\frac{Q_{3V}}{I}(s)$$

$$=\displaystyle\frac{534✕10^{-12}}{1}(s)$$

$$=534✕10^{-12}(s)$$

\(534✕10^{-12}(s)\)は、補助単位を使って表すと\(534ps\)や\(0.534ns\)なので一瞬ですね。

電池の内部抵抗は通常\(1Ω\)（オーム）以下なので、\(3V\)の電池であれば少なくとも最初は\(1A\)以上の電流が流れます。

まだ、だいぶ先になると思いますが、電池とコンデンサーの間に抵抗を入れたときの充電の様子についても書きたいと思っています。

それでは最後に、このコンデンサーに蓄えられた静電エネルギー：\(E_{3V}\)を計算してみます。

〔１〕の投稿で導いた静電エネルギーを求める式に、コンデンサーの容量値：\(178pF\)と電池の電圧：\(3V\)を入れて計算します。

$$E_{3V}=\displaystyle\frac{1}{2}CV^2(J)$$

$$E_{3V}=\displaystyle\frac{1}{2}✕178✕10^{-12}✕3^2(J)$$

$$E_{3V}=801✕10^{-12}(J)$$

\(801✕10^{-12}(J)\)は、補助単位を使って表すと\(801pJ\)や\(0.801nJ\)になります。

次回は、電池の電圧を\(2\)倍の\(6V\)にして計算し、\(3V\)のときの静電エネルギーと比較します。

よろしければ以下のバナーをクリックしていただけると励みになります！

にほんブログ村