電気回路_コンデンサーのエネルギー〔４〕

今回は、コンデンサーに「電荷量：Q」を充電したのちに回路から切り離し、コンデンサーの2枚の板の間隔を変えたときに静電エネルギーがどう変化するかを書いてみます。

前回のおさらい（コンデンサーの2枚の板の間隔を増減）

今回も少し前回のおさらいをしておきます。

前回は、コンデンサーに「出力電圧：V」の定電圧源（電池）を接続して電位差：Vに充電し、次に定電圧源から切り離してコンデンサーの2枚の板の間隔を2倍や1/2にすると、電位差などがどう変化するかを書きました。

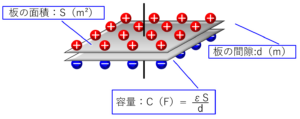
前回使用したのは、下の図になります。

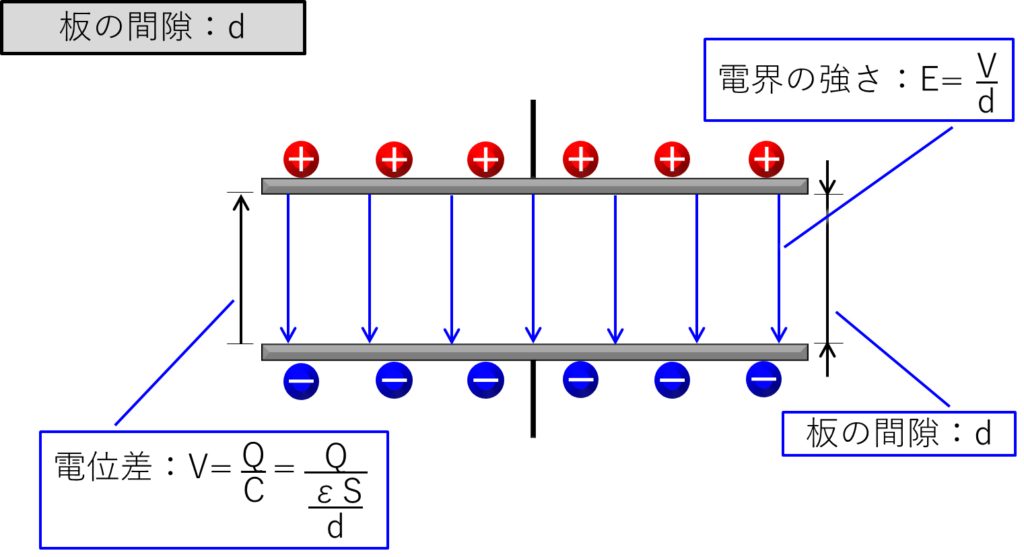
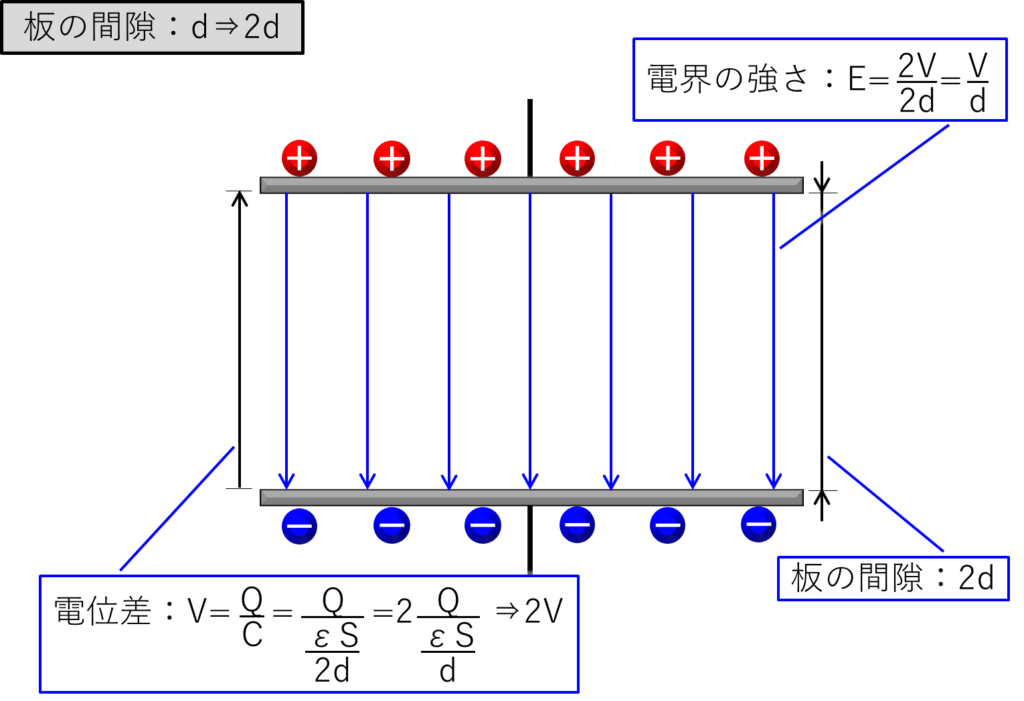
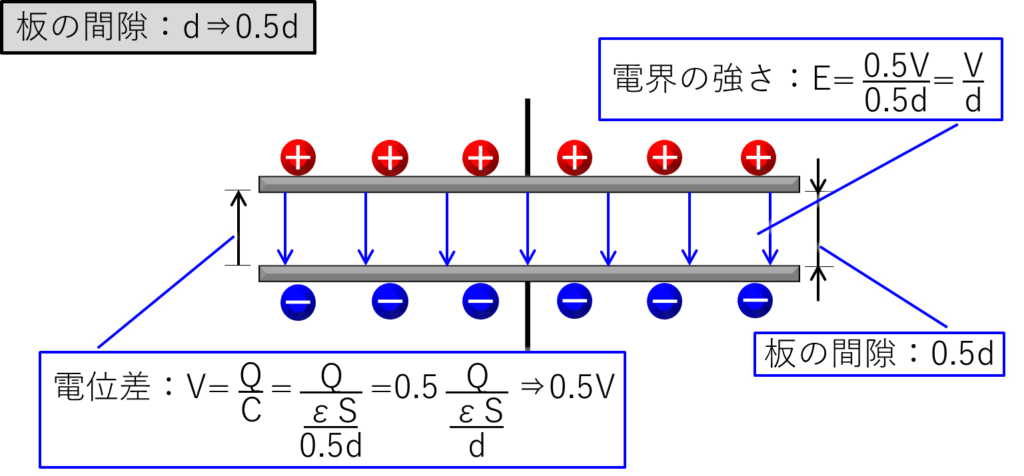
コンデンサーは回路から切り離されているので、コンデンサーに蓄えられた電荷量：Qは一定です。

上の図から、コンデンサーの2枚の板の間隔を2倍にすると、2枚の板の電位差は2倍になることが分かります。

逆にコンデンサーの2枚の板の間隔を1/2にすると、2枚の板の電位差は1/2になります。

そして、2枚の板の間の電界の強さ：E（V/ m）は、電荷量：Qが一定なら変わらないことが分かりました。

2枚の板の間隔を2倍にすると電位差も2倍になるので、電界の強さは変化しないという理屈です。

今回は、2枚の板の間隔を2倍と1/2にすると、コンデンサーに蓄えられた静電エネルギーがどう変化するかを書いてみます。

電荷量：Qが一定のときの静電エネルギー

前回はコンデンサーの2枚の板の間の電界の強さを説明するための図を描きましたが、今回はコンデンサーの容量値：C（単位はF：ファラッド）が変化したときに、電位差：V（絵では電位と記載）がどう変化するかを説明する図を描きました。

まずは、2枚の板の間隔が「d」の時の図です。

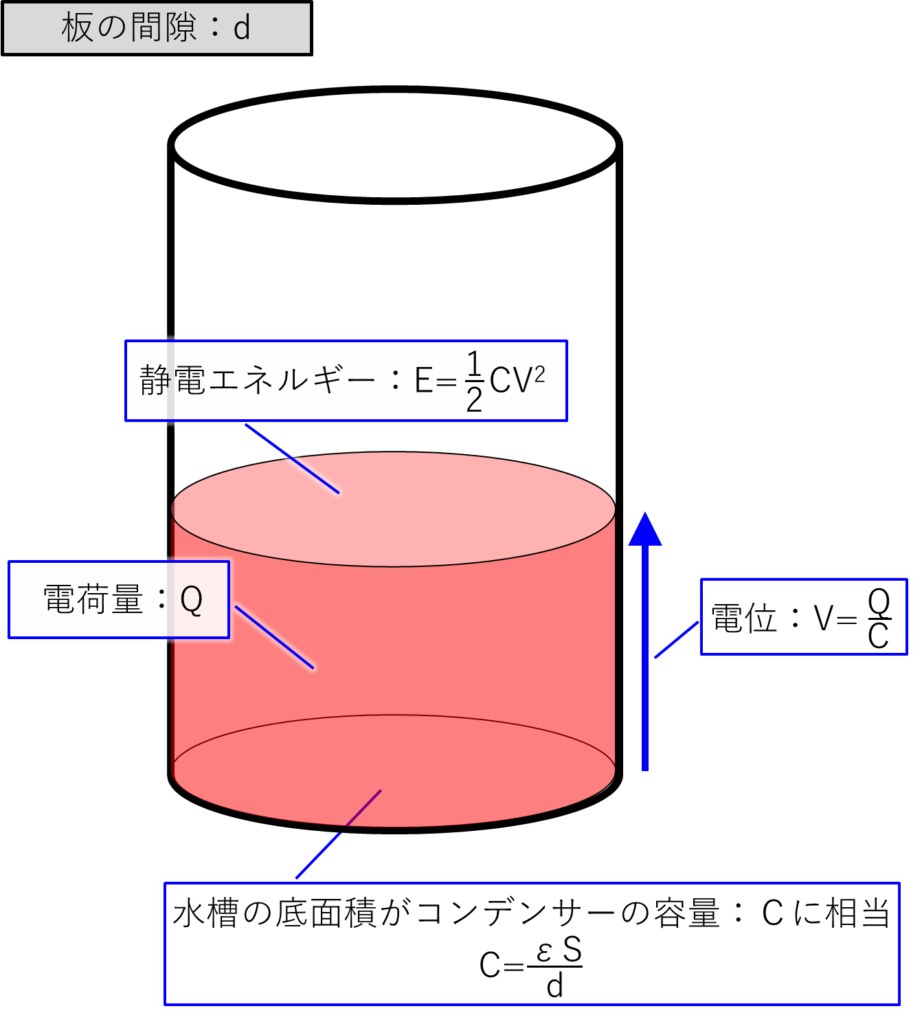
円柱の形をした水槽に電荷がたまっているイメージ図です。

水槽の底面積に相当するのがコンデンサーの容量値：C、たまっている電荷の水位に相当するのが電位：Vと考えると、このコンデンサーに蓄えられた静電エネルギーは「\(E=\displaystyle\frac{1}{2}CV^2\)」です。

これを基本にして、まずは板の間隔を「d ⇒ 2d」に広げると、下の図のようになります。

板の間隔が2倍になると、図に書いたように容量値：\(C_{2d}=\displaystyle\frac{1}{2}C\)となります。

その時、電位：\(V_{2d}=2V\)になります。

この「\(C_{2d}=\displaystyle\frac{1}{2}C\)」と「\(V_{2d}=2V\)」を、「\(E=\displaystyle\frac{1}{2}CV^2\)」に入れて計算すると、\(E_{2d}=2E\)になります。

このことから、2枚の板の間隔を2倍にすると、静電エネルギーも2倍になることが分かります。

次に板の間隔を「d ⇒ 0.5d」に狭めたときの図が下記になります。

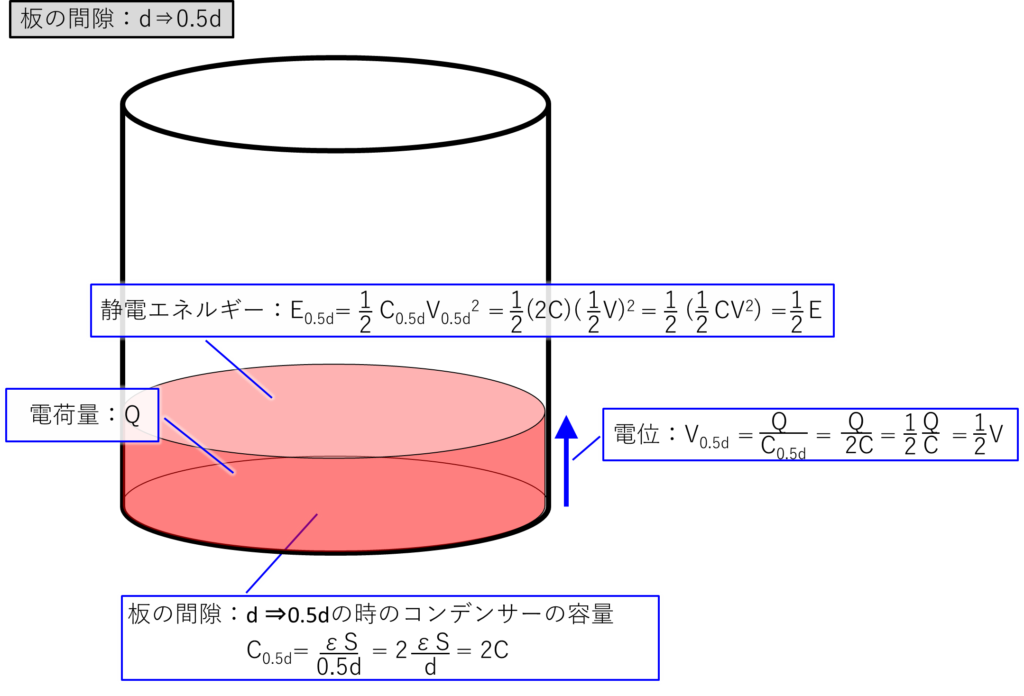
板の間隔が0.5倍になると、図に書いたように容量値：\(C_{0.5d}=2C\)となります。

その時、電位：\(V_{0.5d}=\displaystyle\frac{1}{2}V\)になります。

この「\(C_{0.5d}=2C\)」と「\(V_{0.5d}=\displaystyle\frac{1}{2}V\)」を、「\(E=\displaystyle\frac{1}{2}CV^2\)」に入れて計算すると、\(E_{0.5d}=\displaystyle\frac{1}{2}E\)になります。

このことから、2枚の板の間隔を半分にすると、静電エネルギーも半分になることが分かります。

繰り返しになりますが、コンデンサーに蓄えられた電荷量：Qは一定というのが前提です。

この内容で合っていると思いますが、もし誤りがあれば「お問合せ」からご連絡下さい。

よろしくお願いします。

よろしければ以下のバナーをクリックしていただけると励みになります！

にほんブログ村