抵抗に加えた交流電圧・電流〔２〕（交流電流を抵抗に印加）

前回は抵抗に交流電圧を加えましたが、今回は交流電流を加えてみます。

交流電流源の波形

家庭用電源は、電流が1A未満のスマホ用のUSB電源アダプターに接続しても、10A以上の電流が流れるエアコンに接続しても、常に「VAC=100Vrms」の電圧を供給する交流の定電圧源です。

今回抵抗に接続する交流の電流源は身近には存在しませんが、どのような負荷（抵抗など）に接続しても、常に「IAC=1Arms」を流せる定電流源です。

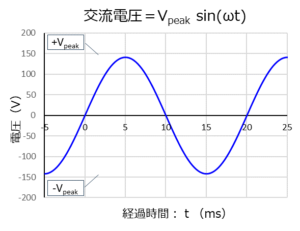
周波数50Hzで「IAC=1Arms」の交流定電流源の波形を下に示します。

電流が変化しているのに「定電流源」というのは矛盾していると思われるかもしれませんが、電流源の実効値「IAC=1Arms」が一定と考えてください。

「V」や「A」のあとにつけている「rms」は、前回書いたように電圧や電流の値が「実効値」であることを表しています。

「実効値」については次回書こうと思います。

想定する回路（交流電流源＋抵抗）

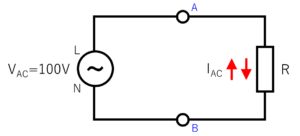
この交流の定電流源に抵抗を接続した回路図は下記になります。

この回路図の左側に描いた丸い回路記号は電流源です。

今回調べて分かったのですが、これは「JIS C 0617」の電流源の回路記号で、直流でも交流でも使えるようです。

今後、電流源にはこの回路記号を使用します。

具体的な数値は「IAC=1Arms」、「R=100Ω」とします。

このときの「VAC」は、オームの法則を使って下の式で計算できます。

$$V_{AC}=I_{AC} R=1✕100=100$$

計算した結果は「VAC=100Vrms」となり、前回の「電圧値」「電流値」と同じです。

交流電流源：IAC(t)に抵抗：Rを接続したときの交流電圧：VAC(t)

次に「実効値」ではなく、瞬間、瞬間で値が変化する「瞬時値」をつないだ波形について書きます。

まずは「電流：IAC(t)」の式を下に示します。

$$I_{AC}(t)=I_{peak}\sin(\omega t)$$

$$=\sqrt{2}✕1\sin(2\pi f t)$$

$$=1.41\sin(2\pi 50 t)$$

$$=1.41\sin(100\pi t)$$

何度も書きますが、「周波数：f=50Hz」で計算しています。

電流の「瞬時値」を、例えば「経過時間：t=5ms=0.005s」で計算すると下記のようになります。

$$I_{AC}(5ms)=1.41\sin(100\pi 0.005)$$

$$=1.41\sin(\displaystyle\frac{\pi}{2})$$

$$=1.41✕1=1.41$$

同様の計算を「経過時間：t=-5ms～25ms」で行った結果が下のグラフになります。

前回と同様、電流の変化を時間経過で表すグラフの左側には、電流波形の「位相（角度）」を表す単位円のグラフを描いています。

「経過時間：t=0」の角度を太い赤線で示しますが、このときの「位相（角度）=0 rad（ラジアン）」です。

次に、「抵抗：R」の両端に生じる「電圧：VAC(t)」の式を下に示します。

$$V_{AC}(t)=I_{AC}(t) R$$

$$=I_{peak}\sin(\omega t)✕R$$

$$=R✕I_{peak}\sin(2\pi f t)$$

$$=100✕\sqrt{2}\sin(2\pi 50 t)$$

$$=141\sin(100\pi t)$$

電流のときと同様、「経過時間：t=-5ms～25ms」で「電圧」の瞬時値を計算した結果を下のグラフに示します。

この結果から、「交流電流電源：IAC(t)」に接続した「抵抗：R」の両端に生じる「交流電圧電源：VAC(t)」も、「交流電流電源：IAC(t)」と同じタイミングで増減することが分かります。

左の単位円のグラフでは、電流と同じように「経過時間：t=0」の角度を太い青線で示しますが、このときの「位相（角度）=0 rad（ラジアン）」です。

「抵抗：R」に接続した「交流電流電源：IAC(t)」と「交流電圧電源：VAC(t)」の位相は、ここでも「位相（角度）=0 rad（ラジアン）」で同じです。

今後は、コンデンサーとコイルに接続した場合と比較していきます。

さて、その前に次回は「実効値」について書こうと思います。

よろしければ以下のバナーをクリックしていただけると励みになります！

にほんブログ村
人気ブログランキング