コイルのインピーダンスの計算式「$Z_L=j \omega L$ 」の求め方（４）

2025年8月12日 2025年8月22日

講師Kazu

今回の投稿は、基本的に前回の『コイルのインピーダンスの計算式「$Z_L=j \omega L$ 」の求め方（３）』と同様ですが、「オイラーの公式」を使って、微分の計算を簡素化しています。

オイラーの公式

「オイラーの公式」は、学生の頃に学んだ記憶が全くなくて、会社に入ってから読んだ本でチラホラと見かけたイメージです。

でも、この公式の重要性をそれなりに理解したのは、ここ10年くらいです。

「オイラーの公式」を下に示します。

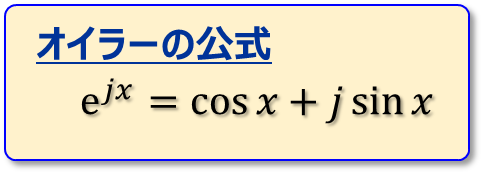
先日書いた下の複素平面の円グラフは、数式「$e^ {j\omega t} $ 」でも表せることは知っていましたが、いつも「なぜだろう」と思っていました。

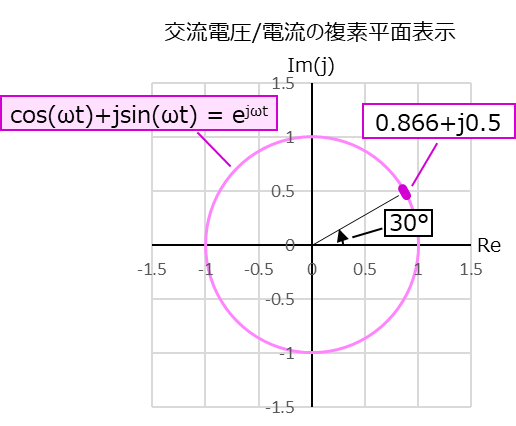
正直なところ、今でも「$e^ {j\omega t} $ 」が複素平面上で円グラフになることはイメージできませんが、理屈としては理解しました。

この公式を使うことで、電流の瞬時値を複素数で表す式は、下のように変形できます。

$$i(t)=I (\cos (\omega t) +j\sin (\omega t)) =Ie^{j\omega t}$$

この式を使って、前回と同じように「コイルのインピーダンスの計算式」を求めますが、その前にもう少し「オイラーの公式」について書いておきます。

オイラーの公式に出てくる「ネイピア数：e 」

まず、オイラーの公式に出てくる「ネイピア数：$e$ 」です。

この数は、「$e=$2.71828…」と小数点以下が無限に続く無理数ですが、無理数の中でも超越数と言われるもので、下の計算式で表せます。

$$e=\lim_{n \to ∞}\left(1+\displaystyle\frac{1}{n}\right)^n$$

この式は、複利の計算式として説明されることが多く、例えば1年で100％の利子がつくと想定し、1年後の預金残高を計算する式と考えることができます。

1万円預金して、利子が1年に1回つく場合は「$n=1$ 」で、1年後の預金残高は下記になります。

$\left(1+\displaystyle\frac{1}{1}\right)^1=2$　　預金残高：2万円

次は半年ごとに利子がつく場合で、「$n=2$ 」で下記になります。

$\left(1+\displaystyle\frac{1}{2}\right)^2=2.25$　　預金残高：2.25万円円

次は1か月ごとに利子がつく場合で、「$n=12$ 」で下記になります。

$\left(1+\displaystyle\frac{1}{12}\right)^{12}=2.6130…$　　預金残高：2.6130…万円

次は1日ごとに利子がつく場合で、「$n=365$ 」で下記になります。

$\left(1+\displaystyle\frac{1}{365}\right)^{365}=2.7145…$　　預金残高：2.7145…万円

そして、「$n=∞$ 」にすると下記になります。

$$e=\lim_{n \to ∞}\left(1+\displaystyle\frac{1}{n}\right)^n=2.71828…$$

これが「ネイピア数」ですが、一例として下のような性質があります。

$$y=e^x$$

$$\displaystyle\frac{dy}{dx}=e^x$$

$$\displaystyle\frac{d^2y}{dx^2}=e^x$$

「ネイピア数：$e$ 」を「$x$乗」した数式は、「$x$ 」で何回微分しても同じ式になります。

これは「ネイピア数：$e$ 」の大きな特徴と思います。

オイラーの公式の求め方

ここで、もう一度オイラーの公式を下に書きます。

$$e^{jx}=\cos x +j\sin x$$

左の「指数関数」と、右の「三角関数」が等しくなるというのも、ちょっとイメージできませんが、べき級数展開を使用した説明で、一応自分は納得しました。

べき級数展開の手順は省略しますが、「$e^x$ 」と「$\sin x$ 」と「$\cos x$」をべき級数展開した結果を下に示します。

$$e^x=1+\displaystyle\frac{1}{1!}x+\displaystyle\frac{1}{2!}x^2+\displaystyle\frac{1}{3!}x^3+\displaystyle\frac{1}{4!}x^4+\displaystyle\frac{1}{5!}x^5+\displaystyle\frac{1}{6!}x^6+\displaystyle\frac{1}{7!}x^+\cdots$$

$$\sin x=\displaystyle\frac{1}{1!}x-\displaystyle\frac{1}{3!}x^3+\displaystyle\frac{1}{5!}x^5-\displaystyle\frac{1}{7!}x^7+\cdots$$

$$\cos x=1-\displaystyle\frac{1}{2!}x^2+\displaystyle\frac{1}{4!}x^4-\displaystyle\frac{1}{6!}x^6+\cdots$$

次に、少し乱暴な気はしますが、「$e^x$ 」の「$x$ 」を「$jx$ 」に置き換えて、「$e^{jx}$ 」を計算します。

$$e^{jx}=1+\displaystyle\frac{1}{1!}jx+\displaystyle\frac{1}{2!}(jx)^2+\displaystyle\frac{1}{3!}(jx)^3+\displaystyle\frac{1}{4!}(jx)^4+\displaystyle\frac{1}{5!}(jx)^5+\displaystyle\frac{1}{6!}(jx)^6+\displaystyle\frac{1}{7!}(jx)^7+\cdots$$

$$e^{jx}=1+\displaystyle\frac{1}{1!}jx-\displaystyle\frac{1}{2!}x^2-\displaystyle\frac{1}{3!}jx^3+\displaystyle\frac{1}{4!}x^4+\displaystyle\frac{1}{5!}jx^5-\displaystyle\frac{1}{6!}x^6-\displaystyle\frac{1}{7!}jx^7+\cdots$$

$$e^{jx}=\left(1-\displaystyle\frac{1}{2!}x^2+\displaystyle\frac{1}{4!}x^4-\displaystyle\frac{1}{6!}x^6+\cdots \right)+j\left(\displaystyle\frac{1}{1!}x-\displaystyle\frac{1}{3!}x^3+\displaystyle\frac{1}{5!}x^5-\displaystyle\frac{1}{7!}x^7+\cdots \right)$$

上の式で、左の（）内は「$\cos x$ 」、右の（）内「$\sin x$ 」の式と同じなので、（）内の式を「$\cos x$ 」と「$\sin x$ 」にして書き換えると下記になります。

$$e^{jx}=\cos x+j\sin x$$

この式が「オイラーの公式」になります。

べき級数展開の手順について知りたい方は、ブルーバックスの『世界は「$e$」でできている』という本を参考にしていただくと良いかもしれません。

この本の内容は、話がわき道に逸れがちなのですが、べき級数展開について分かりやすく書かれていると思います。

「オイラーの公式」に関連しては、もう少し書きたい内容があるのですが、この調子で書いていると、今回もコイルのインピーダンスの計算式について書けなくなりそうなので、今回は止めておきます。

一連の投稿を書き終えたら、今回書きたかった内容を書こうと思います。