コイルのインピーダンスの計算式「$Z_L=j\omega L$」の求め方（３）

2025年8月4日 2025年9月24日

講師Kazu

前回は投稿が長くなり、書ききれなかった内容を今回書きましたが、その内容は、電流の複素数の計算式を微分して、コイルのインピーダンスを計算する式を求めるという内容です。

想定する回路は、下のように交流電圧源の両端にコイルを接続したシンプルな回路です。

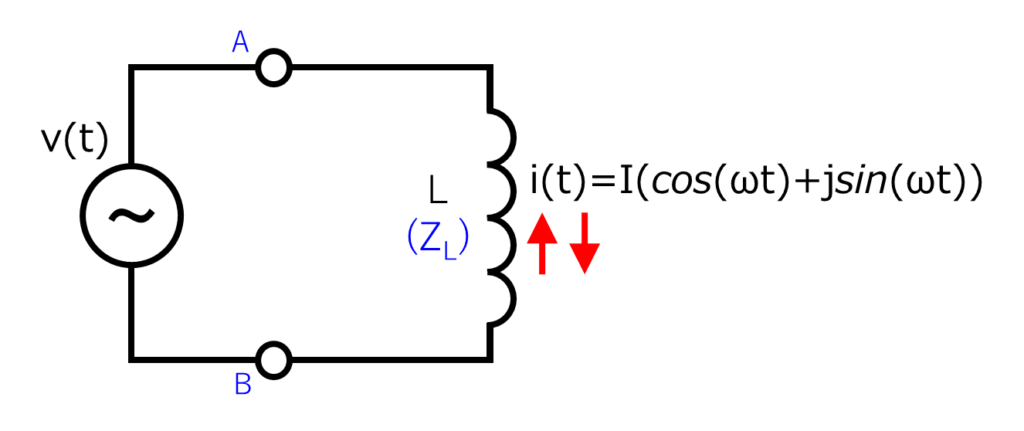
「電圧：$v(t)$ 」と「電流：$i(t)$ 」と「コイルのインダクタンス：$L$ 」の関係式は、「電気回路_コイルの動作【直流】〔２〕」（2023/05/07投稿）などでは「$\Delta$ 」を使って表しましたが、今回は下のように微分を使った式にしました。

$$v(t)=L\displaystyle\frac{di(t)}{dt}$$

前回の投稿では、複素数の説明に電圧「$v(t)=V (\cos (\omega t) + j\sin (\omega t)) $ 」を使いましたが、今回の投稿では電流「$i(t)=I (\cos (\omega t) + j\sin (\omega t)) $ 」を使います。

それではさっそく次の項で、コイルのインピーダンスの計算式を求めていきます。

まず、前の項に書いた「電圧」「電流」「インダクタンス」の関係式から始めます。

$$v(t)=L\displaystyle\frac{di(t)}{dt}$$

この式の「$i(t)$ 」に、電流の瞬時値を複素数で表す式「$i(t)=I (\cos (\omega t) + j\sin (\omega t)) $ 」を入れます。

$$v(t)=L\displaystyle\frac{dI (\cos (\omega t) + j\sin (\omega t))}{dt}$$

「電流振幅：$I$ 」は時間で変化しないので、時間微分の項の前に出します。

$$v(t)=LI\displaystyle\frac{d (\cos (\omega t) + j\sin (\omega t))}{dt}$$

$$v(t)=LI\left(\displaystyle\frac{d (\cos (\omega t))}{dt} + j\displaystyle\frac{d (\sin (\omega t))}{dt}\right) $$

「$\cos (\omega t)$ 」と「$\sin (\omega t)$ 」を「時間：$t$ 」で微分します。

$$v(t)=LI (-\omega \sin (\omega t) + j\omega \cos (\omega t)) $$

「$\omega $ 」を前に出します。

$$v(t)=\omega LI (-\sin (\omega t) + j\cos (\omega t)) $$

「$-\sin (\omega t) $ 」の前の「$-1$ 」に、「$-1=jj$ 」を入れます。

$$v(t)=\omega LI (jj \sin (\omega t) + j \cos (\omega t)) $$

「$j$ 」を前に出します。

$$v(t)=j\omega LI (j\sin (\omega t) + \cos (\omega t)) $$

虚数の「$j\sin (\omega t) $ 」の項を、実数の後ろに移動します。

$$v(t)=j\omega LI (\cos (\omega t) + j\sin (\omega t)) $$

ここで、最初に書いた電流の瞬時値の式の前と後を入れ替えた、「$I (\cos (\omega t) + j\sin (\omega t)) =i(t)$ 」を上の式に入れます。

$$v(t)=j\omega L i(t) $$

最後にこの式を使って、コイルのインピーダンスの計算式「$Z_L=\displaystyle\frac{v(t)}{i(t)}$ 」を求めます。

$$Z_L=\displaystyle\frac{v(t)}{i(t)}$$

上の式に「$v(t)=j\omega L i(t)$ 」を入れます。

$$Z_L=\displaystyle\frac{j\omega L i(t)}{i(t)}$$

$$Z_L=j\omega L$$

今回の方が、コイルのインピーダンスの計算式の求め方としては比較的一般的な方法と思います。

次回は、今回の計算をもっとシンプルに行う方法について書こうと思います。

おそらく、次回書く方法が、最も一般的な方法と思います。

よろしければ以下のバナーをクリックしていただけると励みになります！

コイルのインピーダンスの計算式「\(Z_L=j\omega L\)」の求め方（３）