電気回路_コイルの動作【直流】〔２〕

前回は、コイルのインダクタンス：\(L\)について書いたので、今回はそのコイルに直流の定電圧源を接続してみます。

コイルに定電圧源を接続

コイルに定電圧源を接続したイメージを、回路図にすると下のようになります。

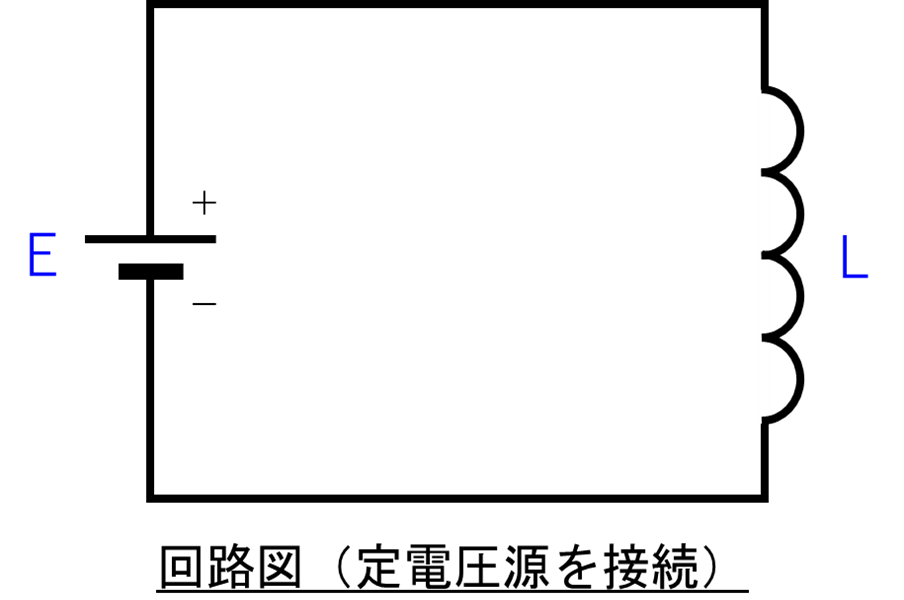
電気回路を知っている人は、「こんな接続をするとコイルが焼ける」と不安になると思います。

自分もそう思います。

実際にこの回路を組むと、コイルから煙が出てきて、いやな臭いがしそうなので、絶対に試さないでください。

この回路図のコイルは理想的なもので、どれだけ流れる電流が増えても壊れないものとします。

左の定電圧源も理想的なもので、どれだけ流れる電流が増えても出力電圧：\(E\)(V)を維持できるものとします。

このときのコイルの電圧と電流を縦軸、経過時間を横軸にしてグラフ化すると、下のようになります。

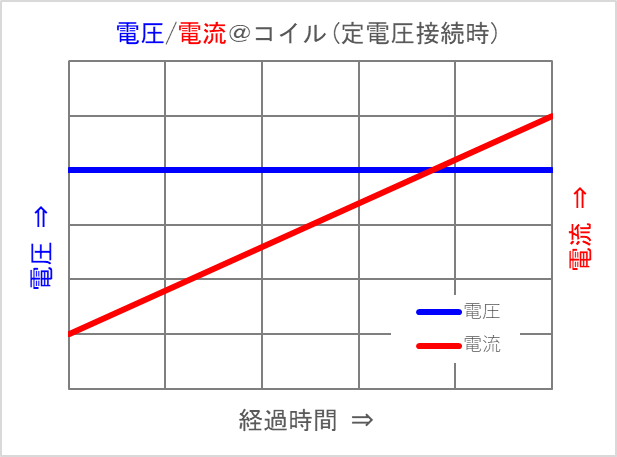
コイルに定電圧を与えたとき、コイルに流れる電流は一定の傾斜で増えていきます。

比較のため、コンデンサーに定電圧を与えたときの回路図とグラフも書いておきます。

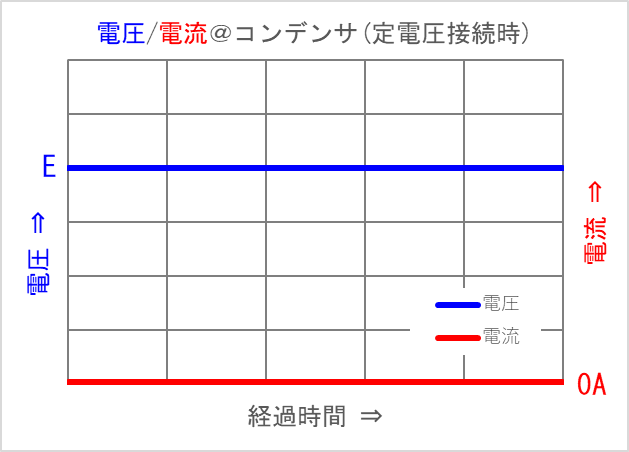
コンデンサーに定電圧を与え続けると、コンデンサーに流れる電流は0A（アンペア）になり、コンデンサーに電流は流れなくなります。

コイルに定電圧源を接続した瞬間のシミュレーション結果

次に、コイルに流れる電流の変化を具体的な数値を入れてグラフを作成してみます。

コイルの両端の電圧は最初は0Vとし、次の瞬間に定電圧源から1Vを与えたとします。

また、コイルのインダクタンス：Lは1H（ヘンリー）とします。

先ほど、この回路は絶対に試さないでくださいと書きましたが、実際に組み立てるのではなく、プログラムでシミュレーションすることは可能です。

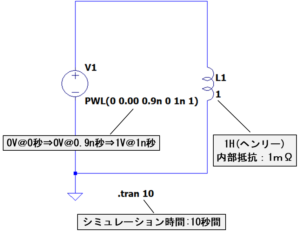
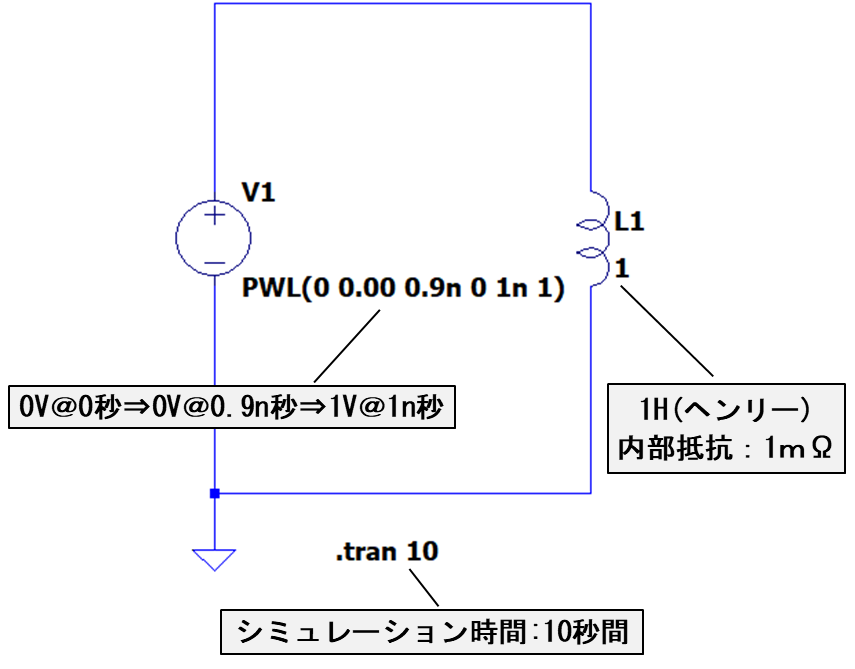
先ほど書いた定電圧源や、コイルの条件を下に示します。

〔定電圧源〕

0秒 ⇒ 0.9n秒 ：0V（ボルト）

0.9n秒 ⇒ 1n秒：0V ⇒ 1V

1n秒以降 ：1V

〔コイル〕

インダクタンス：1H（ヘンリー）

コイル内部の直流抵抗：1mΩ

定電圧源の出力電圧は、0.9n秒 ⇒ 1.0n秒の0.1n秒の間に、0Vから1Vに上昇します。

0.1n秒は、「一瞬」という意味で決めた時間ですが、「n秒」の「n」は「ナノ」で、\(10^{-9}\)を表す補助単位です。

そのため、0.1n秒は、\(0.1✕10^{-9}=1✕10^{-10}\)秒となり、とても短い時間です。

0.1n秒は、真空中の光でも3cmしか進めない時間です。

また、コイル内部の直流抵抗は、シミュレーターの初期値の1mΩとしました。

シミュレーションに使用した回路図は下記になります。

この回路で、コイル両端の電圧値と電流値を時間軸でシミュレーションした結果を下に示します。

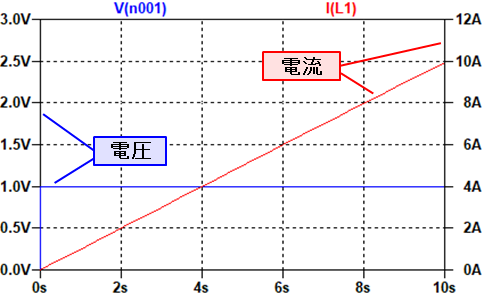
横軸は経過時間で、左端が0秒、右端が10秒です。

左の縦軸は電圧値で、0秒では0Vですが、次の瞬間には1Vに変化しています。

右の縦軸は電流値で、電流は右肩上がりに増加しており、その傾斜は1秒当たり1Aなので1A/s（アンペア_パー_セカンド）です。

コイルの電圧：Ｅ、電流：Ｉ、インダクタンス：Ｌ、経過時間：ｔの間には、下の関係式が成り立ちます。

$$E=L\displaystyle\frac{ΔI}{Δt}$$

今回はコイルに定電圧を与えているので、この式を下のように変形します。

$$\displaystyle\frac{ΔI}{Δt}=\displaystyle\frac{E}{L}$$

この\(E\)に\(1V\)、\(L\)に\(1H\)を入れると下記になります。

$$\displaystyle\frac{ΔI}{Δt}=\displaystyle\frac{E}{L}=\displaystyle\frac{1(V)}{1(H)}=1(A/s)$$

コンデンサーに定電圧源を接続したときのシミュレーション結果

ついでに、コンデンサーに定電圧源を接続したときのシミュレーション結果も書いておきます。

シミュレーションの条件はコイルの場合と同様とし、コンデンサーの値は下記とします。

〔コンデンサー〕

キャパシタンス：１Ｆ（ファラッド）

コンデンサー内部の直流抵抗：無限大

定電圧源の出力は、コイルと同じとします。

シミュレーションに使用した回路図は下記になります。

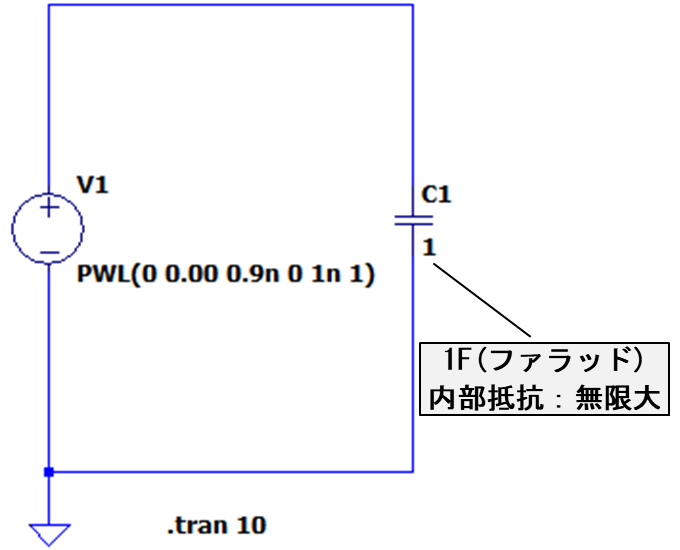
この回路で、コンデンサー両端の電圧値と電流値を時間軸でシミュレーションした結果を下に示します。

コイルのときと同様、横軸は経過時間、左の縦軸は電圧値です。

右の縦軸は電流値ですが、0秒付近では10GA（ギガアンペア）という、とんでもない電流値になっています。

その後の電流値は0Aです。

GA（ギガアンペア）のG（ギガ）も補助単位で、\(10^9\)を表します。

上の0秒付近を拡大したグラフを下に示します。

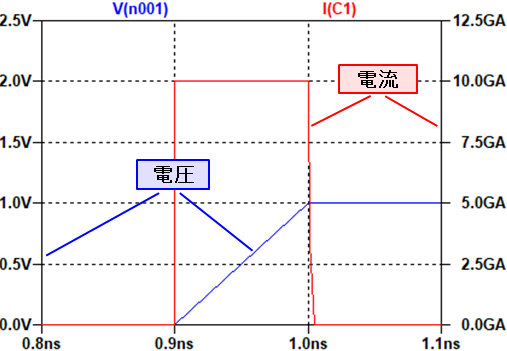
定電圧源の出力電圧は、経過時間：0.9ns ⇒ 1.0nsで0V ⇒ 1Vに上昇しており、コンデンサー両端の電圧も同じです。

この0.1nsの間、コンデンサーには10GA（ギガアンペア）の電流が流れていることが、このグラフから分かります。

1F（ファラッド）のコンデンサーの両端の電圧が1V（ボルト）変化するためには、コンデンサーに1C（クーロン）の電荷が流れ込む必要があります。

これは、以前の記事で書いた\(Q=CV=1(C)\)を計算した結果です。

それが、0.1nA（ナノアンペア）の間に流れ込むので、その時の電流値は下の式で求まります。

$$I=\displaystyle\frac{ΔQ}{Δt}=\displaystyle\frac{1(C)}{0.1(ns)}=\displaystyle\frac{1(C)}{0.1✕10^{-9}(s)}=10✕10^9(A)$$

電流は、1秒間に流れる電荷量：Q（C_クーロン）なので、\(0.1✕10^{-9}s\)（秒）の間に\(1C\)（クーロン）の電荷が流れると、上の式で計算したように\(10GA\)（ギガアンペア）の電流が流れることになります。

電流：\(I\)、電荷量\(C\)、時間：\(t\)の関係式は、自分は\(Q=It\)がイメージしやすいので、先ほどの\(Q=CV\)ととも頭にイメージできると忘れないと思います。

次回は、定電流源を接続します。

よろしければ以下のバナーをクリックしていただけると励みになります！

にほんブログ村