電気回路_抵抗〔６〕ブリッジ回路（テブナンの定理_前半）

テブナンの定理を使って、不平衡ブリッジ回路に流れる電流値を計算で求めます。

今回の計算で求める電流値

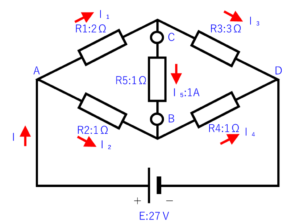
今回は、テブナンの定理を使って下の不平衡ブリッジ回路の「I₅」の電流値を計算で求めます。

テブナンの定理の「V₀」を計算

「R5」に流れる電流「I₅」を求めるために、前回の投稿「テブナンの定理の使い方」に書いたように、まずは「R5」を取り外したときのCとBの間の電圧「V₀」を計算します。

少しおさらいしておくと、上の回路を下の回路のようにシンプルな等価回路にして、そこに「R₅」を取り付けて「I₅」を計算します。

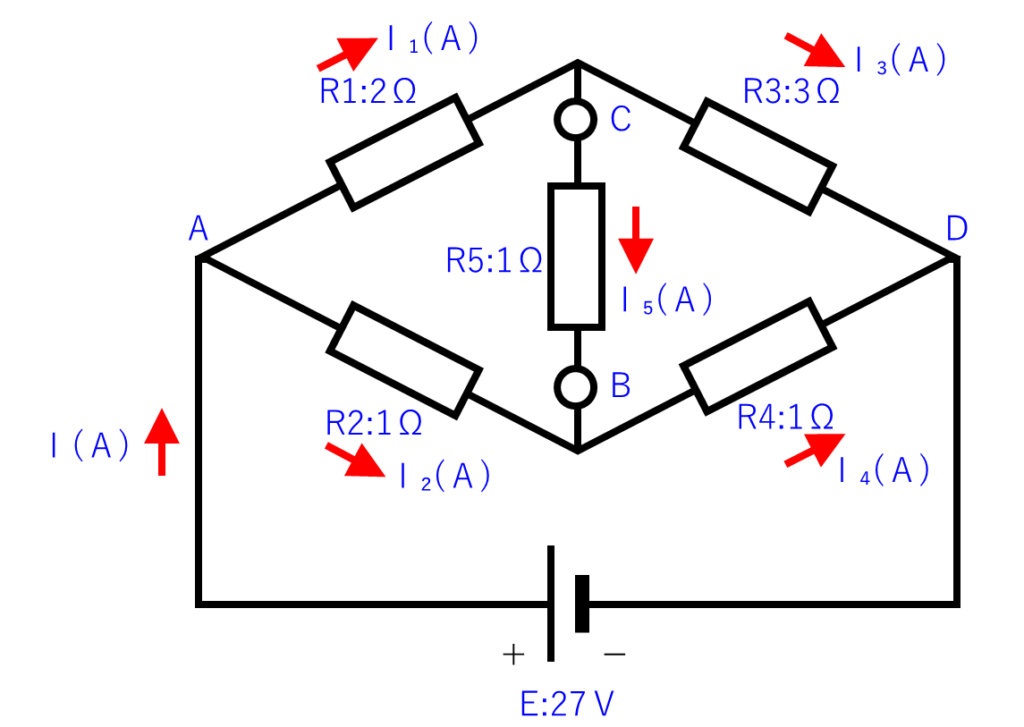
もう一度、上の回路図を下に置きますが、ひし形部分を四角形にした回路図をその下に描きました。

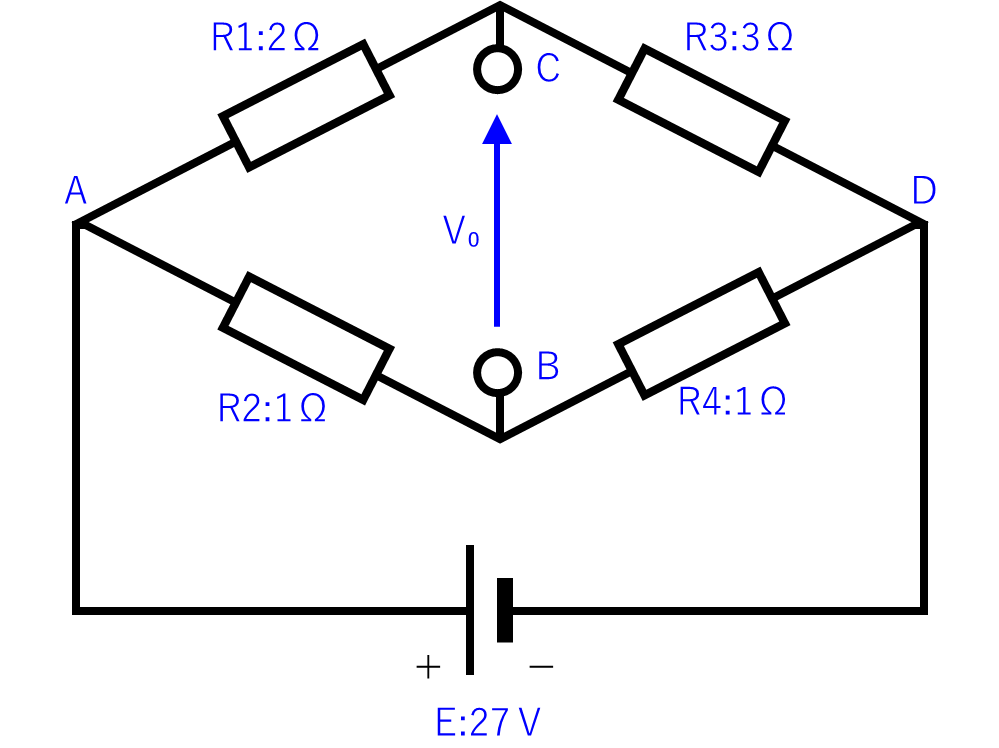
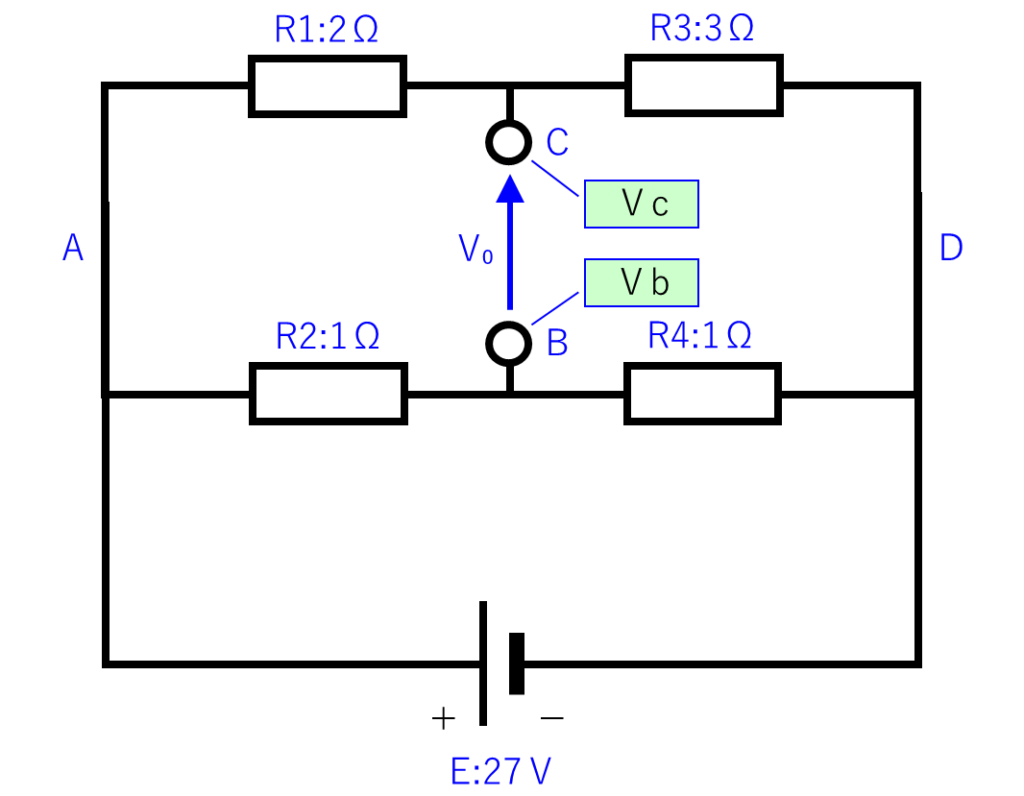
この回路図の「Vc」と「Vb」を求めて引き算すれば、「V₀」が求まります。

最初に「Vc」を計算してみましょう。

$$Vc=\displaystyle\frac{E}{R1＋R3}×R3＝\displaystyle\frac{27}{2＋3}×3=16.2(V)$$

「E」を「R1＋R3」で割って「R1＋R3」に流れる電流を求め、それにR3を掛ければ「Vc」が求まります。

同様にして「Vb」を計算します。

$$Vc=\displaystyle\frac{E}{R2＋R4}×R4＝\displaystyle\frac{27}{1＋1}×1=13.5(V)$$

「Vc-Vb」を計算して「V₀」を求めます。

$$V₀=Vc-Vb=16.2-13.5=2.7(V)$$

テブナンの定理の「R₀」を計算

次に等価回路の「R₀」を求めます。

最初の回路図をもう一度下に置きます。

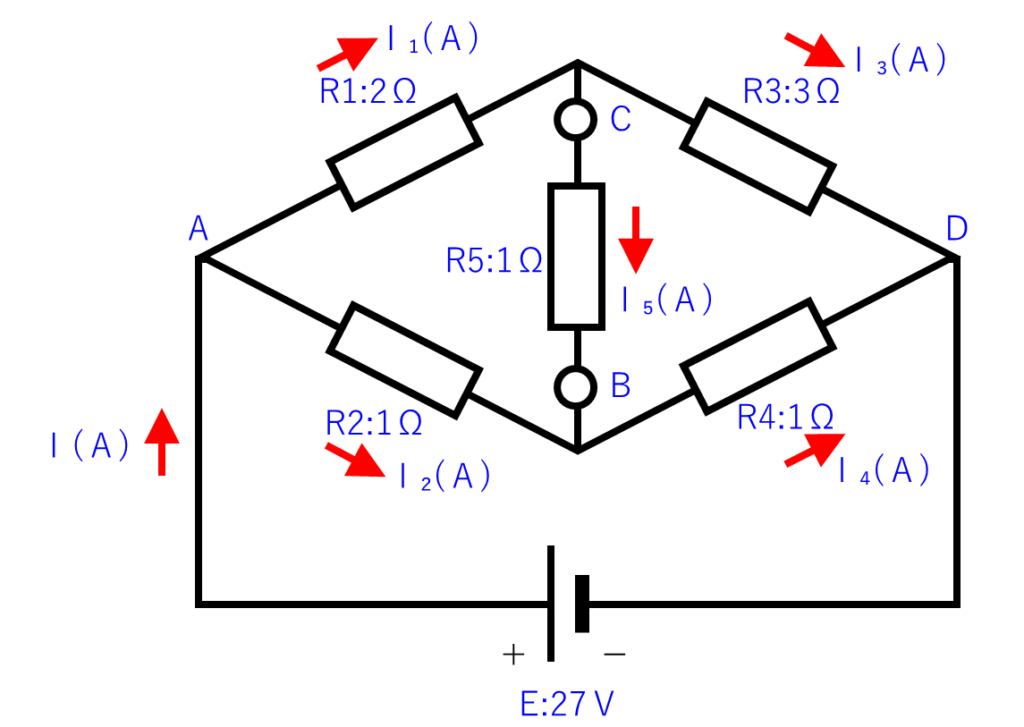
この回路図から「R₅」を取り外し、下の電池（定電圧源）を「0Ω」の配線に置き換えて、CとBの間の抵抗値を計算します。回路図は下のようになります。

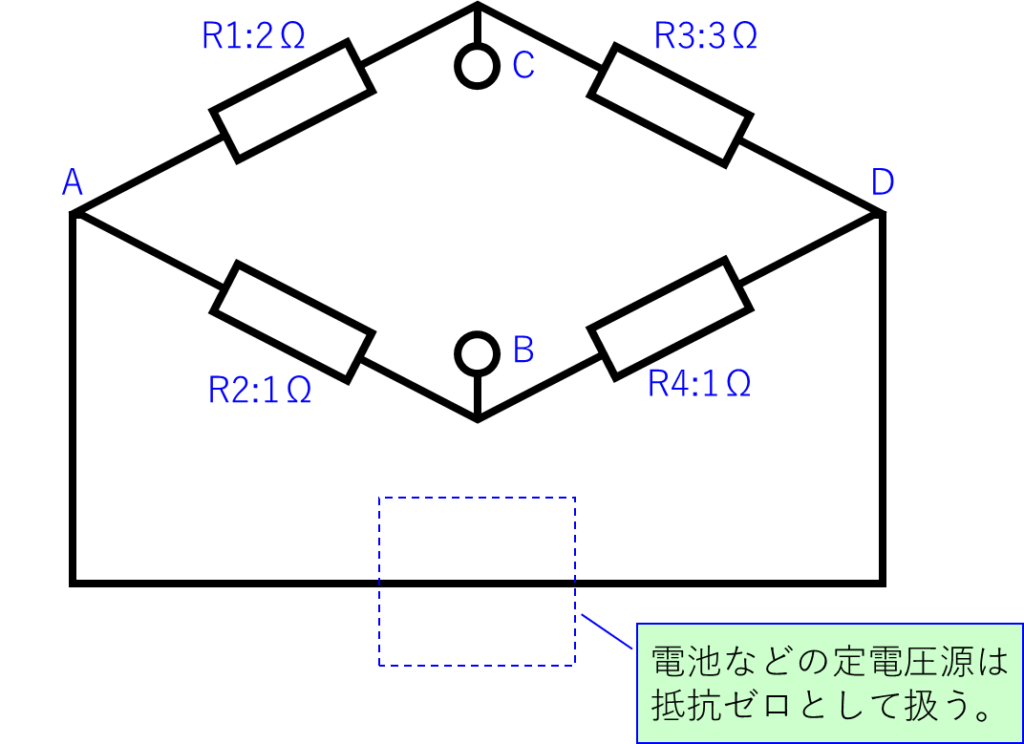
C-B間の抵抗値の計算をするときにイメージしやすいよう、回路図を下のように変形します。

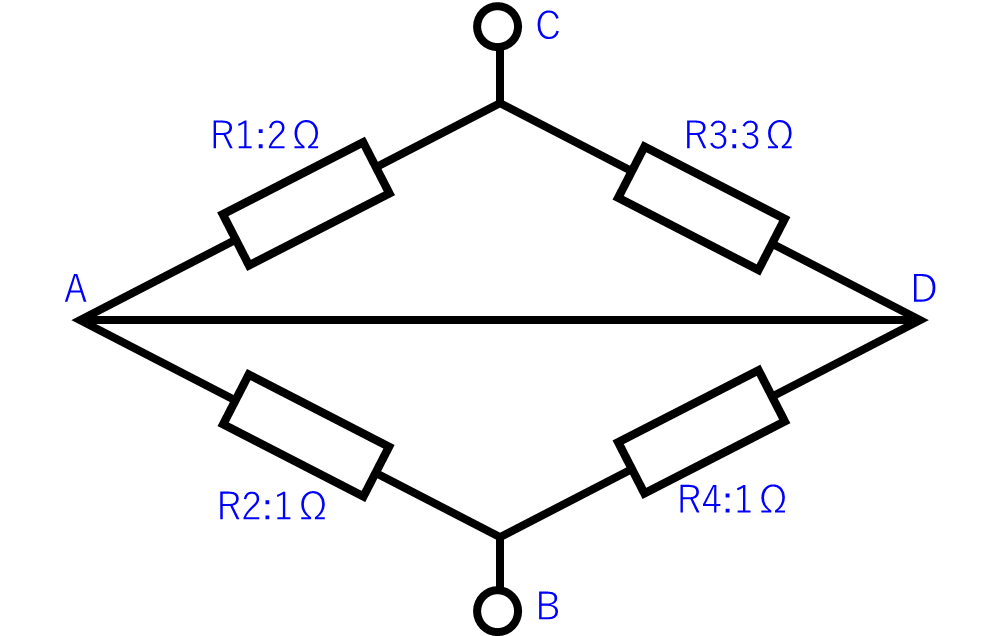
さらに、回路図を下のように変形すると、C-B間の抵抗「R₀」は「R1」と「R3」、「R2」と「R4」の並列抵抗を計算して、足し合わせれば求まることが分かります。

「R₀」を計算します。

$$R_0=\displaystyle\frac{1}{\displaystyle\frac{1}{R1}+\displaystyle\frac{1}{R3}}＋\displaystyle\frac{1}{\displaystyle\frac{1}{R2}+\displaystyle\frac{1}{R4}}=\displaystyle\frac{R1R3}{R3+R1}+\displaystyle\frac{R2R4}{R4+R2}$$

$$=\displaystyle\frac{2×3}{3+2}+\displaystyle\frac{1×1}{1+1}=\displaystyle\frac{6}{5}+\displaystyle\frac{1}{2}=\displaystyle\frac{12+5}{10}=1.7(Ω)$$

「V₀」「R₀」「R5」から「I₅」を計算

計算して求めた「V₀」「R₀」を使って、「I₅」を計算します。

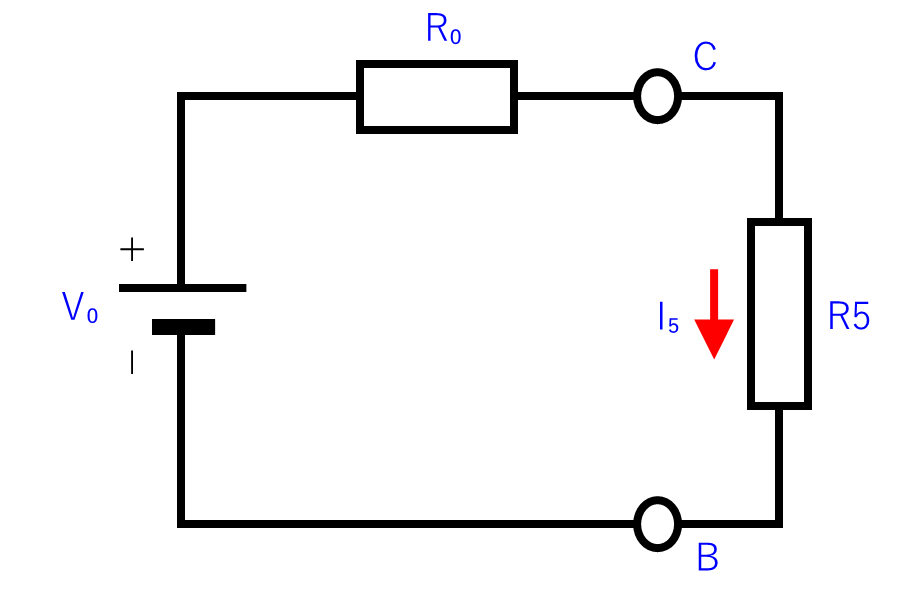
$$I_5=\displaystyle\frac{V_0}{R_0+R5}=\displaystyle\frac{2.7}{1.7+1}=\displaystyle\frac{2.7}{2.7}=1(A)$$

テブナンの定理を使って、不平衡ブリッジ回路の真ん中の抵抗に流れる電流値「I₅」を求めました。

ここから一気に「I₁～I₄」を求めていくのですが、奥さんから1回の投稿が長すぎて読みづらいと指導をうけたので、それは次回書こうと思います。

よろしければ以下のバナーをクリックしていただけると励みになります！

にほんブログ村