電気回路_抵抗〔7〕ブリッジ回路(テブナンの定理_後半)
テブナンの定理を使って、不平衡ブリッジ回路に流れる電流値を計算で求める完結編です。
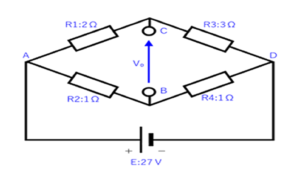
今回の計算する電流値
前回はテブナンの定理を使って、下の不平衡ブリッジ回路の「I₅」の電流値を計算しました。
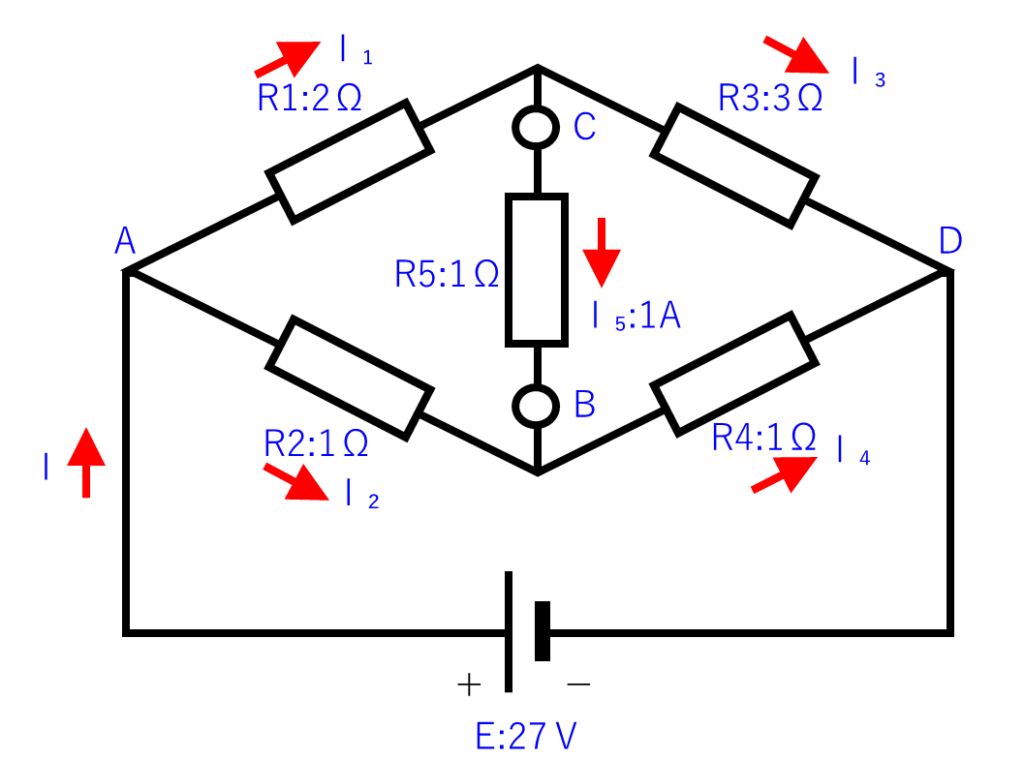
真ん中の縦の抵抗:R₅に流れる電流は1Aだと分かったので、これを使って「I」や「I₁~I₄」の電流値を計算します。
「I₁とI₃」を計算
「R1」と「R3」の両端の電圧を足すと27Vになるのことから、下の式を立てることができます。
$$E=R1×I_1+R3×I_3$$
ここで「I₁=I₅+I₃」なので、上の式の「I₁」に「I₅+I₃」を代入します。
$$E=R1×(I_5+I_3)+R3×I_3=R1×I_5+(R1+R3)×I_3$$
ここで、「E=27」「R1=2」「R3=3」「I₅=1」を入れてI₃を求めます。
$$27=2×1+(2+3)×I_3=2+5×I_3$$
$$I_3=\displaystyle\frac{27-2}{5}=5(A)$$
次に「I₁=I₅+I₃」に「I₅=1」「I₃=5」を入れてI₁を求めます。
$$I_1=I_5+I_3=1+5=6(A)$$
「I₂とI₄とI」を計算
もう一度、上の回路図を下に描いておきます。
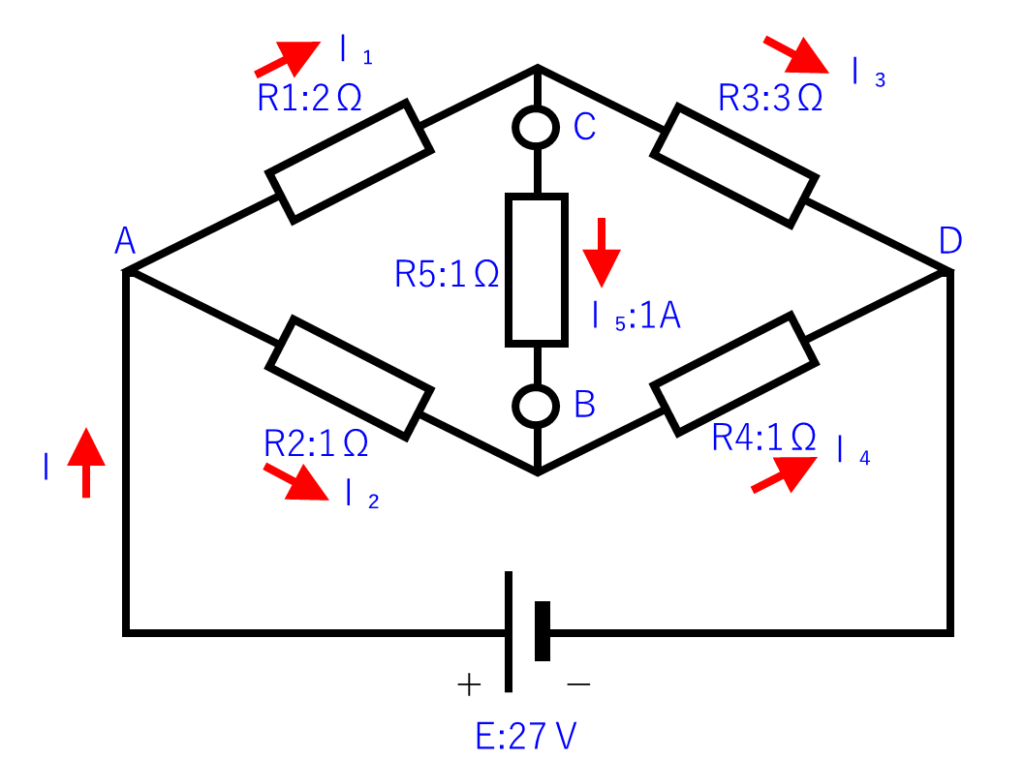
先ほどと同様、「R2」と「R4」の両端の電圧を足すと27Vになるのことから、下の式を立てることができます。
$$E=R2×I_2+R4×I_4$$
ここで「I₄=I₂+I₅」なので、上の式の「I₄」に「I₂+I₅」を代入します。
$$E=R2×I_2+R4×(I_2+I_5)=(R2+R4)×I_2+R4×I_5$$
ここで、「E=27」「R2=1」「R4=1」「I₅=1」を入れてI₂を求めます。
$$27=(1+1)×I_2+1×1=2×I_2+1$$
$$I_2=\displaystyle\frac{27-1}{2}=13(A)$$
次に「I₄=I₂+I₅」に「I₂=13」「I₅=1」を入れてI₄を求めます。
$$I_4=I_2+I_5=13+1=14(A)$$
「I=I₁+I₂」で「I」を計算します。
$$I=I_1+I_2=6+13=19(A)$$
まとめ
抵抗と定電圧源を使って、合成抵抗や電流、電圧を計算してみました。
今回は、テブナンの定理を使ってR5に流れる電流値を求めて、それから他の電流値を計算しましたが、例えばR3に流れる電流値をテブナンの定理を使って求めて、それから他の電流値を求めることもできます。ただ、少し計算の量が増えます。
他にも定電流源を含んだ回路にテブナンの定理を使う方法や、定電圧源と定電流源が混在した回路にテブナンの定理を使用する方法も書いてみようかと思いましたが、そろそろ飽きられていると思うので止めておきます。
もしニーズがあれば、「お問合せ」からリクエストしていただければと思います。
次回からは、コンデンサーやコイルについて書いていこうと思います。
よろしければ以下のバナーをクリックしていただけると励みになります!
にほんブログ村