電気回路_コンデンサーの動作【直流】〔３〕

前回はコンデンサーに定電圧源を接続しましたが、今回は定電流源を接続してみます。

コンデンサーに定電流源を接続すると・・

コンデンサーに定電流源を接続した回路図を下に示します。

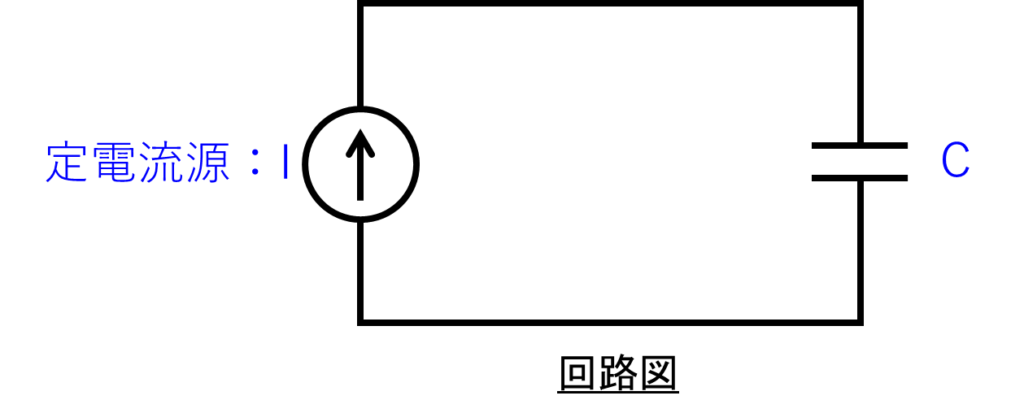
左の定電流源から矢印の方向に一定の電流が流れ、右のコンデンサーに電荷がたまります。

次に、回路図をコンデンサーをイメージした構造イメージ図を下に示します。

定電流源は、プラスの電荷（正電荷）を矢印の方向に流しますので、コンデンサーの上の板には正電荷が、下の板にはマイナスの電荷（負電荷）がたまっていきます。

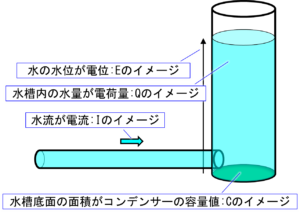
そうすると、コンデンサーに蓄えられる電荷：Qは増えていきますので、下の式から分かるようにコンデンサーの両端の電位差：Eは大きくなっていきます。

$$E=\displaystyle\frac{Q}{C}$$

コンデンサー両端の電位差は、時間の経過とともに大きくなりますが、その様子は経過時間を「t（s）」とすると下の式で計算できます。

$$E=\displaystyle\frac{Q}{C}=\displaystyle\frac{It}{C}$$

これまでに書いたかもしれませんが、電流は1秒間に流れる電荷の量なので、1秒間に1C（クーロン）の電荷が流れたら1A（アンペア）、1秒間に10C（クーロン）の電荷が流れたら10Aです。

このことから電流は、I＝Q/t（Q：電荷量、I：電流、t：時間）という式で表せます。

これを変形するとQ=Itになるので、上の式の「Q」に「Q=It」を入れました。

コンデンサーの両端の電位差がどう変化するかを考えるときに、自分は「Q=CV」と「Q=It」という式をよく使うので、覚えておいた方が良いと思います。

覚えるといっても、イメージ通りの関係式なので覚える必要がないかもしれませんが・・。

定電流源に接続したコンデンサーを水槽に例えると・・

定電流源に接続したコンデンサーを、水槽に例えた絵を描いたので下に示します。

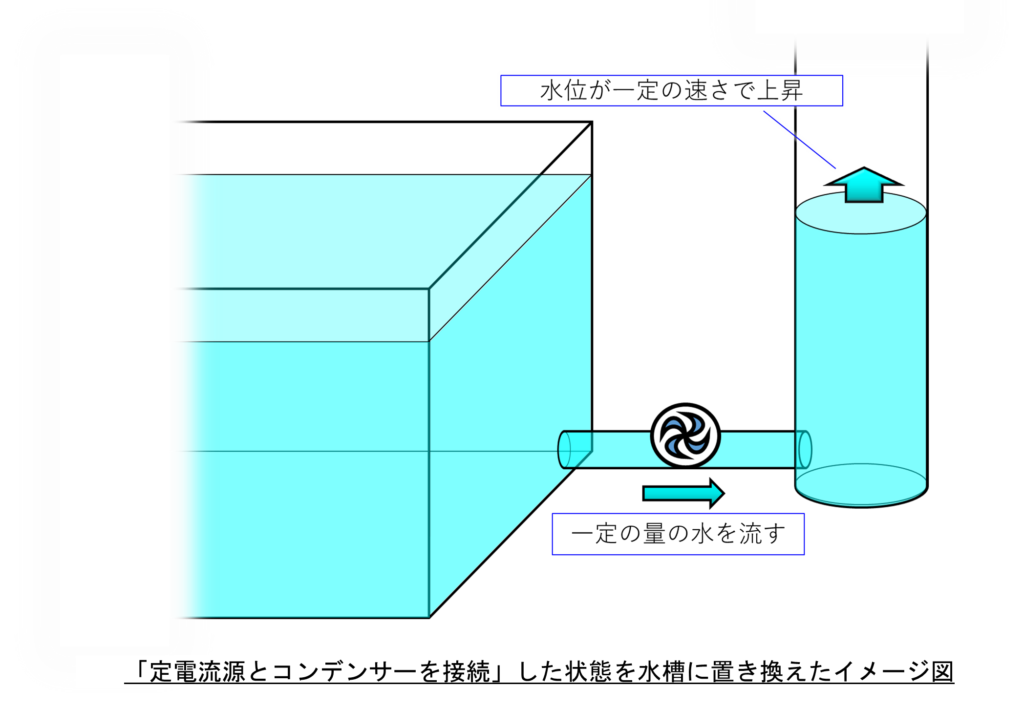
左側の大きな水槽と、右側の小さめの水槽の間をつなぐパイプに描いた回転羽根のような絵は、水を一定のペースで左から右に流すポンプのイメージ図です。

そうすると、右の小さめの水槽の水面は一定のペースで上昇します。

この水面の上昇は、先ほどの「E」が時間の経過とともに上昇する計算式と一致します。

$$E=\displaystyle\frac{It}{C}$$

この計算式では、時間が経過するとコンデンサーの電位差「E」が上昇しますが、そのスピードはコンデンサーの容量値「C」が大きくなると緩やかになります。

コンデンサーの容量値「C」は、前回と同様に右側の小さめの水槽の底の面積に相当すると考えると、水槽の底の面積が大きくなるほど水位の上昇が緩やかになることでも一致します。

コンデンサーの電圧と電流のグラフ

この様子を、横軸を経過時間、左側縦軸を電圧、右側縦軸を電流にしたグラフを下に示します。

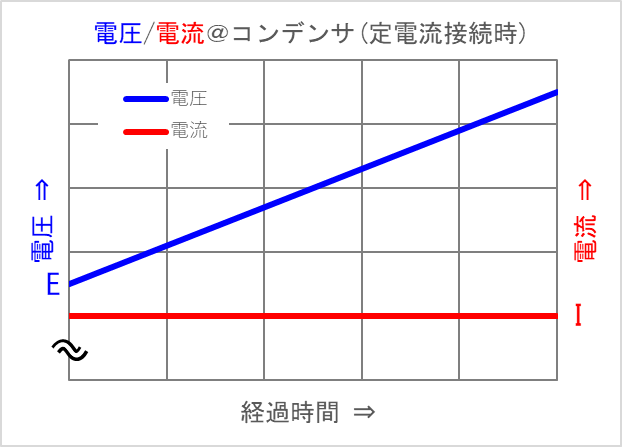
このグラフは、定電流源をコンデンサーに接続して十分な時間が経過したあとの、コンデンサーの電圧と、回路に流れる電流を表しています。

常に一定の電流がコンデンサーに流れると、コンデンサーの両端の電位差が時間の経過とともに大きくなっていきます。

ちなみに実際のコンデンサーに理想的な定電流源を接続しておくと、コンデンサーの両端の電位差が上がり過ぎてコンデンサーを壊してしまいますのでご注意ください。

現在書いている投稿のテーマにも、そろそろ微分や積分の考え方を使っていきたいと思いますので、あまり得意ではないのですが、次回からは微分や積分について何回か書いてみようと思います。

よろしければ以下のバナーをクリックしていただけると励みになります！

にほんブログ村