直流と交流の違い〔１１〕（最初から積分で求める交流電源の消費電力計算式）

2023年12月5日 2024年2月10日

講師Kazu

前回の投稿では、一度「$\lim \sum $」で表した式を積分の式にするという面倒なことをしましたが、今回は最初から積分の式を使って解きます。

交流電源の「電圧」と「電力」と「電力量」の式

何度も登場しますが、家庭用交流電源の電圧の変化を表すグラフです。

ここでは、主に東日本で使用されている50Hzの交流電源を想定したので、周期は20msになります。

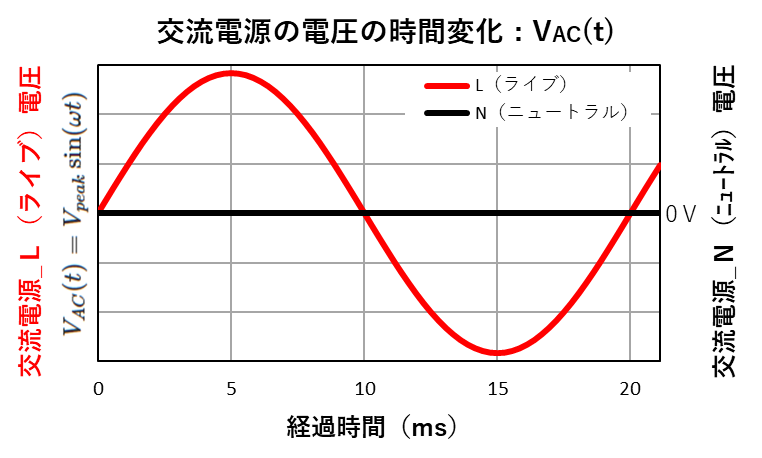
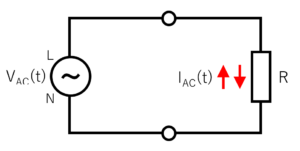
この電圧変化を「$V_{AC}(t)$」として、この電源に抵抗「$R$」を接続したときに流れる電流を「$I_{AC}(t)$」とします。

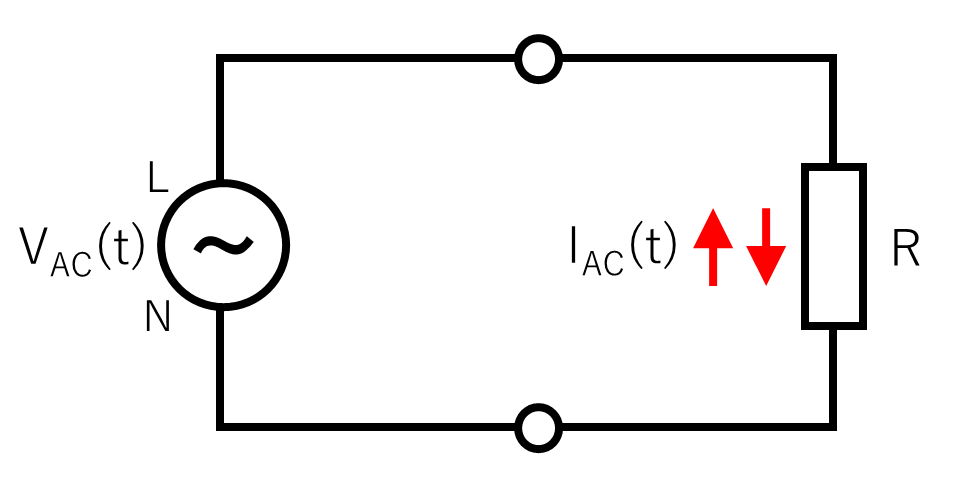
このとき、抵抗「$R$」で消費される電力「$P_{AC}(t)$」は、下記の式で表せます。

$$P_{AC} (t)=V_ {AC} (t)✕ I_ {AC} (t)$$

$$=V_ {AC} (t)✕ \displaystyle\frac{V_ {AC} (t)}{R}$$

$$= \displaystyle\frac{V^2_ {AC} (t)}{R}$$

この式の「$V_{AC}(t)$」に、上のグラフの縦軸に書いている「$V_ {peak} \sin (\omega t)$」を入れると下の式になります。

$$P_{AC} (t)= \displaystyle\frac{(V_ {peak} \sin (\omega t))^{2}}{R}$$

この式をグラフにすると下のようになります。

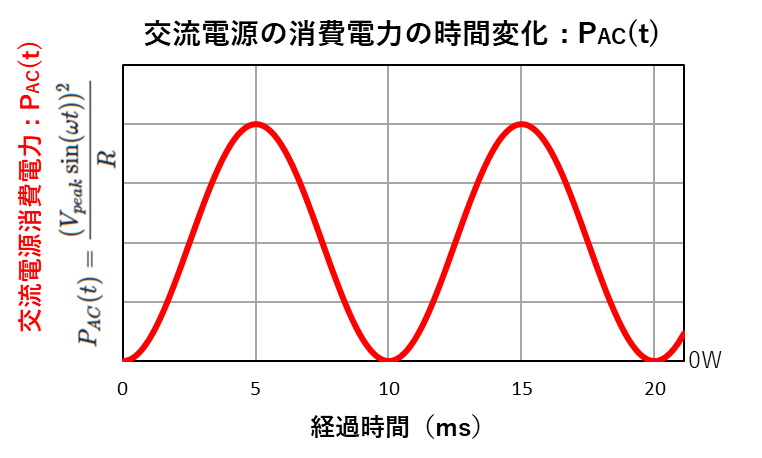
これから、この電力の平均値を計算していきますが、最初に0～20msまで1周期分の電力量を計算し、それを周期：20msで割り算して電力の平均値を求めます。

電力量というのは、消費電力と時間の掛け算で求めますが、グラフにすると下の赤い部分の面積になります。

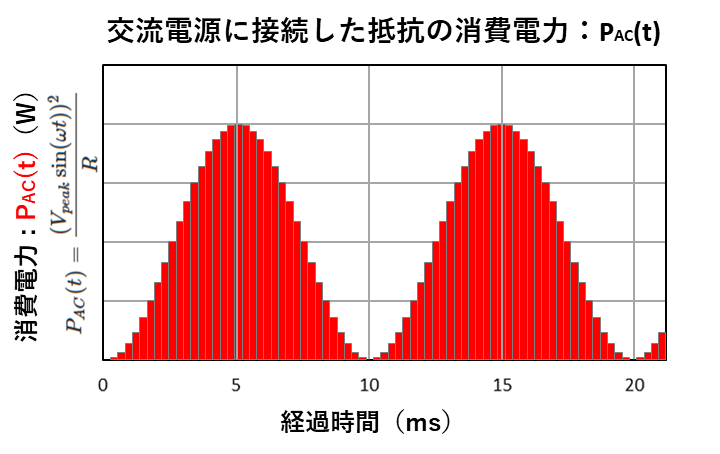
この面積は、「$P_{AC}(t)$ 」を時間で積分すると求まります。

イメージは、上のグラフに示したように、0～20msを細かく分割して短い時間「$dt$」にし、その短い時間「$dt$」と消費電力「$P_{AC}(t)$」を掛け算し、最後にそれらを全て足し合わせて面積を求めます。

これが積分です。

これを積分の式で表すと、下記になります。

$$E_{(0～T)}= \int_{0}^{T}\displaystyle\frac{(V_ {peak} \sin (\omega t))^{2}}{R}\, dt$$

「$E_{(0～T)}$ 」は0から20msまでの赤い部分の面積で、電力量（エネルギー）になります。

積分の計算

ここでも前々回の投稿と同様、「$\sin^2 α$」を「$\cos β$」で表す2倍角の公式を使います。

使用する公式は下記になります。

$$\cos 2x=1-2\sin^2 x$$

この式を少し変形します。

$$\sin^2 x=\displaystyle\frac{1-\cos 2x}{2}$$

この式を使って、前の項の「$E_{(0～T)}$」の式を解いていきます。

まず「$E_{(0～T)}$」の式を下に書きます。

$$E_{(0～T)}= \int_{0}^{T}\displaystyle\frac{(V_ {peak} \sin (\omega t))^{2}}{R}\, dt$$

次に、「$t$」が変化しても変わらない電圧値や抵抗値を前に出します。

$$E_{(0～T)}=\displaystyle\frac{V^2_ {peak}}{R} \int_{0}^{T} \sin^2 (\omega t)\, dt$$

先ほどの「2倍角の公式」を使うと下記になります。

$$E_{(0～T)}=\displaystyle\frac{V^2_ {peak}}{R} \int_{0}^{T} \left(\displaystyle\frac{1-\cos 2\left(\omega t \right)}{2}\right)\, dt$$

ここでも、「$t$」が変化しても変わらない分母の「$2$」を前に出します。

$$E_{(0～T)}=\displaystyle\frac{V^2_ {peak}}{2R} \int_{0}^{T} \left(1-\cos \left(2 \omega t \right) \right) \, dt$$

積分の公式の「$\int \, dx=x + C$」と「$\int \cos ax \, dx=\displaystyle\frac{1}{a} \sin ax + C$」を使用すると下記になります。

$$E_{(0～T)}=\displaystyle\frac{V^2_ {peak}}{2R} \left[t-\displaystyle\frac{1}{2 \omega}\sin \left(2 \omega t \right) \right] _{0} ^{T}$$

積分の手順に従い、「$t$」に「$T$」と「$0$」を入れて引き算します。

$$E_{(0～T)}=\displaystyle\frac{V^2_ {peak}}{2R} \left(\left(T-\displaystyle\frac{1}{2 \omega}\sin \left(2 \omega T \right) \right) -\left(0 -\displaystyle\frac{1}{2 \omega}\sin \left(2 \omega 0 \right) \right) \right) $$

「$\omega=2\pi f$」を入れて、解いていきます。

$$E_{(0～T)}=\displaystyle\frac{V^2_ {peak}}{2R} \left(\left(T-\displaystyle\frac{1}{2 \omega}\sin \left(2 (2\pi f) T \right) \right) -\left(-\displaystyle\frac{1}{2 \omega}\sin 0 \right) \right) $$

$$E_{(0～T)}=\displaystyle\frac{V^2_ {peak}}{2R} \left(\left(T-\displaystyle\frac{1}{2 \omega}\sin \left(4\pi f T \right) \right) -\left(-\displaystyle\frac{1}{2 \omega} 0 \right) \right) $$

周波数「$f$」と周期「$T$」の掛け算は「$1$」になるので、計算を続けます。

$$E_{(0～T)}=\displaystyle\frac{V^2_ {peak}}{2R} \left(T-\displaystyle\frac{1}{2 \omega}\sin \left(4\pi 1 \right) \right) $$

$$E_{(0～T)}=\displaystyle\frac{V^2_ {peak}}{2R} \left(T-\displaystyle\frac{1}{2 \omega}\sin \left(4\pi \right) \right) $$

「$\sin 4\pi=0$」を入れて続けます。

$$E_{(0～T)}=\displaystyle\frac{V^2_ {peak}}{2R} \left(T-\displaystyle\frac{1}{2 \omega} 0 \right) $$

$$E_{(0～T)}=\displaystyle\frac{V^2_ {peak}}{2R} T $$

この式が0からT（20ms）までの電力量なので、これを「$T$」で割って消費電力の平均値を求めます。

$$P_{AC}=\displaystyle\frac{E_{(0～T)}}{T}$$

$$P_{AC}=\displaystyle\frac{\displaystyle\frac{V^2_ {peak}}{2R} T}{T}$$

$$P_{AC}=\displaystyle\frac{V^2_ {peak}}{2R}$$

今回も、前回の投稿と同じ結果です。

次回こそは「直流と交流の違い」の最終回にしたいと思います。