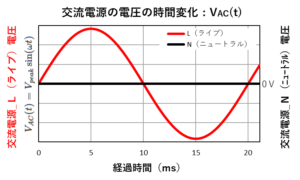
直流と交流の違い〔１２〕（AC100VのVpeak：141Vの算出）

『直流と交流の違い〔２〕』で、『家庭用交流電源の電圧は、「\(+141V\)」から「\(-141V\)」まで変化するのに、なぜ\(AC100V\)なのか』と書きましたが、今回はそれを説明していきます。

これまでのおさらい

『直流と交流の違い〔２〕』は、もう何か月も前に書いた内容なので、少しおさらいします。

まず最初に直流電圧源：\(V_{DC}=100V\)と、それに接続した抵抗：\(R\)の回路図を下に示します。

このとき、抵抗：\(R\)で消費する電力：\(P_{DC}\)は下の式で計算できます。

$$P_{DC}=V_{DC}✕I_{DC}$$

$$=V_{DC}✕\displaystyle\frac{V_{DC}}{R}$$

$$=\displaystyle\frac{V^2_{DC}}{R}$$

次に交流電圧源：\(V_{AC}=100V\)と、それに接続した抵抗：\(R\)の回路図を下に示します。

このとき、抵抗：\(R\)で消費する電力：\(P_{AC}\)は、前回までの投稿で求めた下の式で計算できます。

$$P_{AC}=\displaystyle\frac{V^2_{peak}}{2R}$$

この式の「\(V_{peak}\)」は、前回までの投稿で使用した交流電圧源が時間的に変化することを表す式「\(V_{AC}(t)=V_{peak}\sin(\omega t)\)」の「\(V_{peak}\)」です。

直流電圧源：\(V_{DC}=100V\)に接続した抵抗：\(R\)で消費する電力：\(P_{DC}\)と、同じ抵抗：\(R\)に接続した交流電圧源：\(V_{AC}=100V\)による消費電力：\(P_{AC}\)は等しくなるように決められているので、「\(P_{DC}=P_{AC}\)」となる「\(V_{peak}\)」を計算すると、「\(+141V\)」と「\(-141V\)」が出てきます。

「Vpeak」の計算

それでは、さっそく計算していきます。

まずは、「\(P_{DC}=P_{AC}\)」の式から始めます。

$$P_{DC}=P_{AC}$$

この式に、前の項で書いた「\(P_{DC}=\displaystyle\frac{V^2_{DC}}{R}\)」と「\(P_{AC}=\displaystyle\frac{V^2_{peak}}{2R}\)」を入れます。

$$\displaystyle\frac{V^{2}_{DC}}{R}=\displaystyle\frac{V^2_ {peak}}{2R}$$

両辺の分母に「\(R\)」があるので、両辺に「\(R\)」を掛けて「\(R\)」を消します。

$$V^{2}_{DC}=\displaystyle\frac{V^2_ {peak}}{2}$$

右辺と左辺を入れ替えます。

$$\displaystyle\frac{V^2_ {peak}}{2}=V^{2}_{DC}$$

両辺に「\(2\)」を掛けます。

$$V^{2}_{peak}=2V^2_ {DC}$$

両辺をルートして、平方根を求めます。

$$V_{peak}= \sqrt {2} V_{DC}$$

「\(V_{DC}=100V\)」を入れて、数値計算を行います。

$$V_{peak}= 1.4142...✕100V$$

$$V_{peak} ≒ 141V$$

これを、「\(V_{AC}(t)=V_{peak}\sin(\omega t)\)」に入れると、「\(\sin(\omega t)\)」の最大値と最小値は「\(+1\)」と「\(-1\)」になるので、家庭用交流電圧源「\(V_{AC}\)」の最大値と最小値は、「\(+141V\)」と「\(-141V\)」になります。

経過時間を横軸にした「\(V_{DC}\)」と「\(V_{AC}\)」の波形のグラフを、最後にもう一度のせておきます。

これで、「直流と交流の違い」は終了にします。

これからは、交流についてさらに詳しく書いていこうと思います。

よろしければ以下のバナーをクリックしていただけると励みになります！

にほんブログ村
人気ブログランキング