微分や積分の話【積分（１）】

コンデンサーやコイルの話を書くのに、そろそろ微分や積分が必要になるので、ここで書きます。

微分と積分

電気回路に限らず、物理現象を考えるときにはやはり微分と積分は必要になると思います。

自分もそんなに詳しくありませんが、これからの投稿にいきなり微分や積分を使うのも良くないかなと思うので、自分の分かる範囲で書いておきます。

加速度と速度と移動距離

微分や積分は、「加速度」「速度」「移動距離」の関係で説明するのがよいように思います。

学校の授業では、下の計算式が出てきたと思います。

$$加速度(m/s^2)=a$$

$$速度(m/s)=v=at+V_0$$

$$移動距離(m)=s=\displaystyle\frac{1}{2}at^2+V_0t+S_0$$

【記号の説明】

・a(m/s²)：加速度（速度が1秒間にa(m/s)ずつ変化）

・v(m/s)：t秒経過後の速度（1秒間に一定の方向に進む距離）

・t(s)：時間（単位は秒）

・V₀(m/s)：t=0秒時点での速度

・s(m)：t秒経過後の移動距離

・S₀(m)：t=0秒時点での移動距離

今回は計算を簡単にしたいので、V₀(m/s)とS₀(m)は「ゼロ」で話を進めます。

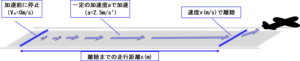
飛行機の離陸を想定

今回は、空港の滑走路を離陸する飛行機を想定します。

一般的な旅客機は、離陸する滑走路に到着すると一度停止し、それから加速していって離陸します。

ネットで調べたところ、加速度の平均値は2.5m/s²、離陸までの時間は30秒くらいのようです。

この条件で、飛行機が離陸するときの速度や、離陸までの移動距離を計算します。

ただ、まだ絵が描けていないので、この内容の投稿は来週書こうと思います。

今回は、次回の計算に使う「1からｎまでの和を求める公式」について書きます。

「1からｎまでの和を求める公式」

「1からｎまでの和」は、テレビでも時々でてくる「1+2+‥＋10」を簡単に計算する方法の拡大版です。

「1+2+‥＋10」の計算結果は、「1+10=11」「2+9＝11」「3+8=11」「4+7＝11」「5+6＝11」の合計で55になります。

「nが10ではなくて、奇数の場合は？」と思われるかもしれません。

この場合、例えば「1+2+‥＋11」の計算を省略せずに書くと次のようになります。

$$「1+11=12」$$

$$「2+10＝12」$$

$$「3+9=12」$$

$$「4+8＝12」$$

$$「5+7＝12」$$

$$「6+6=12」$$

$$「7+5＝12」$$

$$「8+4=12」$$

$$「9+3＝12」$$

$$「10+2＝12」$$

$$「11+1＝12」$$

これらを合計して2で割ると「1+2+‥＋11」が求まるので、12×11÷2=66となります。

これを一般的な式にすると下記になります。

$$「1からｎまでの和」=\displaystyle\frac{(1+(n))+(2+(n-1))+(3+(n-2))+‥+((n-1)+2)+((n)+1)}{2}=\displaystyle\frac{n(n+1)}{2}$$

分子は(n+1)がn個あるのでn(n+1)となり、それを半分にすると「1からｎまでの和」になります。

これを図で説明すると次のようになります。

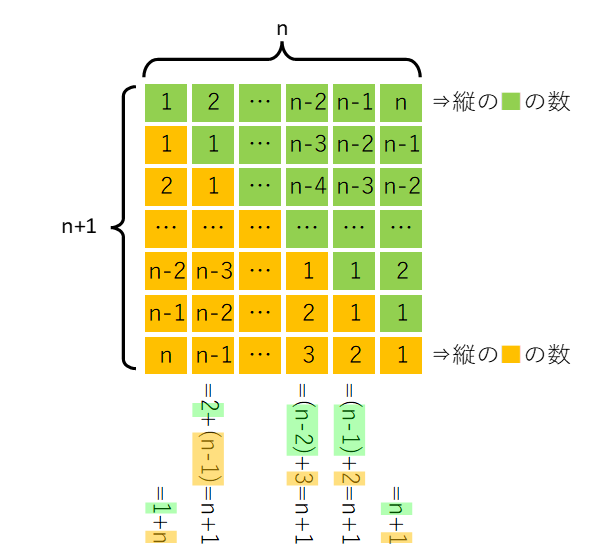
横には「□」がn個あり、縦には「□」が(n+1)個ありますので、「□」の合計はn×(n+1)個になります。

「1からｎまでの和」は、このn×(n+1)個の「□」の1/2なので下の式になります。

$$「1からｎまでの和」=\displaystyle\frac{n(n+1)}{2}$$

これはΣという記号を使うと下のように書くこともできます。

$$「1からｎまでの和」=\sum_{k=1}^{n} k =1+2+…+k+…+(n-1)+n=\displaystyle\frac{n(n+1)}{2}$$

「Σk」は「1+2+…+(n-1)+n」のことになりますが、「k」の値は「Σ」の下の「k=1」から「Σ」の上の「k=n」までの全ての自然数で、これらの総和になります。

上の絵は、こちらの方が分かりやすいかなと描いてみましたが分かりづらいかもですね。

次回はこの公式を使って、飛行機の離陸の話を書こうと思います。

よろしければ以下のバナーをクリックしていただけると励みになります！

にほんブログ村