ドラム缶に蓄えた水の位置エネルギー(積分)
積分の考え方を使って、ドラム缶に蓄えた水の位置エネルギーを計算する式を求めてみます。
今回計算する水の位置エネルギー
以前の位置エネルギーの投稿では、質量:\(m\)の物質が高さ:\(h\)の位置にあるとき、その物質の位置エネルギー:\(E\)は「\(E=mgh\)」で計算できると書きました。
「\(g\)」は重力加速度で、値は\(9.8m/s^2\)です。
今回使用するドラム缶のイメージ図を下に示します。
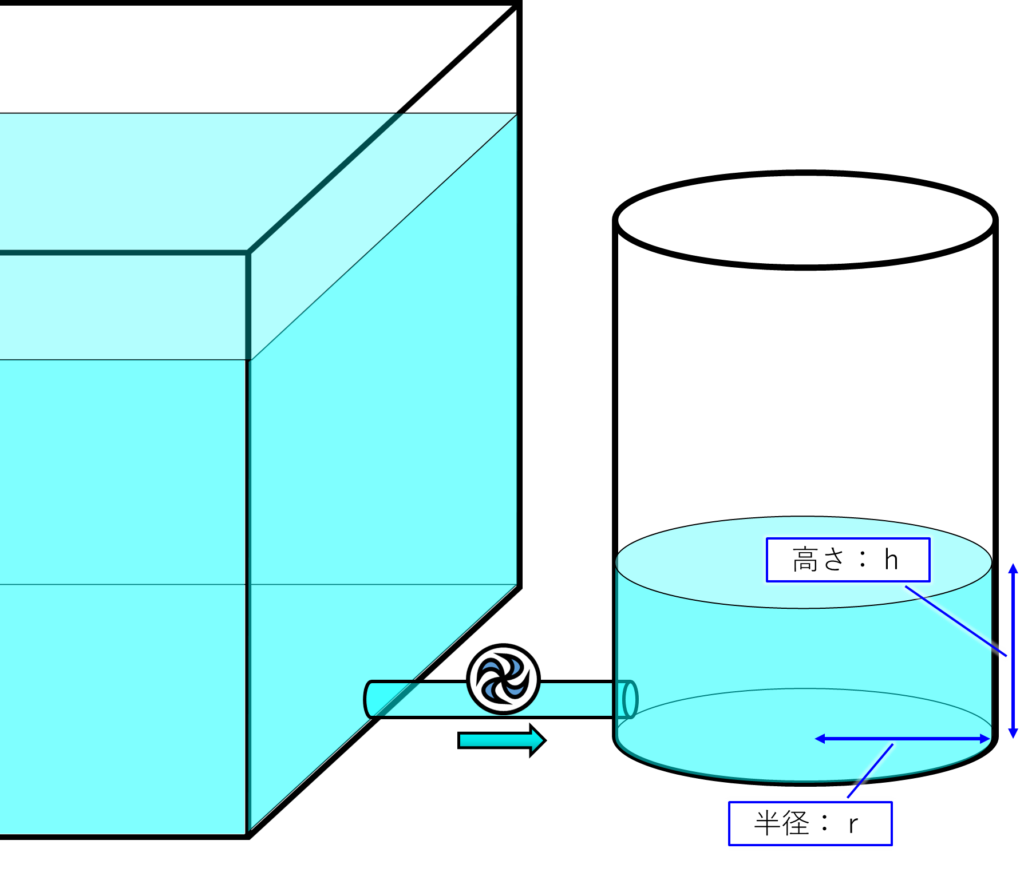
左の大きなタンクから、下の管を通してドラム缶に水を送り込みます。
このときのドラム缶の底面の高さを\(0m\)として、このドラム缶に蓄えた水の位置エネルギー\(E\)を計算します。
まず、水の体積:\(V\)を水面の高さ:\(h\)とドラム缶の半径:\(r\)で表すと下記になります。
$$V=πr^2h$$
式を見やすくするために、ドラム缶の底面積:\(πr^2\)を\(S\)とすると下の式になります。
$$V=Sh$$
ドラム缶に蓄えた水の位置エネルギー
ドラム缶に蓄えた水の水面の高さ:\(h\)を横軸、ドラム缶の底面が水から受ける荷重:\(F\)を縦軸にしたグラフを描くと下記になります。

これまでは、青い四角形の棒を下から上に描いていましたが、今回は同じようには描けなかったので、左から右に描いてみました。
左下から右上に伸びている赤い線は下の式で表せます。
$$F=ρShg$$
この式で使用している記号の説明をします。
\(F\):ドラム缶の底が水から受ける荷重で単位は\(N\)(ニュートン)です。
\(ρ\):水の密度(単位体積当たりの質量)で、約\(1000kg/m^3\)です。
\(S\):ドラム缶の底面積で\(πr^2\)で求まり、単位は\(m^2\)です。
\(h\):ドラム缶の底面から水面までの高さです。
\(g\):重力加速度で約\(9.8m/s^2\)です。
上の式の右辺の単位を計算すると下のようになります。
$$(kg/m^3)×(m^2)×(m)×(m/s^2)=kgm/s^2=N$$
ちなみに水の密度を表す記号:\(ρ\)は「ロー」と読みます。
これまでのように、横軸の高さを「\(n\)」分割すると、分割したひとつの高さは「\(\displaystyle\frac{h}{n}\)」になります。
そのとき分割した円盤状の水一枚の荷重は「\(ρS\displaystyle\frac{h}{n}g\)」になります。
水の円盤一枚の荷重「\(ρS\displaystyle\frac{h}{n}g\)」に高さ「\(\displaystyle\frac{h}{n}k\)」をかけると位置エネルギーになるので、これらの円盤の「\(1\)」個目から「\(n\)」個目までの位置エネルギーを全て足し合わせれば、ドラム缶に蓄えた水の全体の位置エネルギーになります。
これを表す計算式を書きます。
$$E=\lim_{n \to ∞}{\sum_{k=1}^{n} \left(ρS\displaystyle\frac{h}{n}g\right)\left(\displaystyle\frac{h}{n}k\right)}$$
ここまで書いて、グラフだけだと分かりづらいように思いました。
ドラム缶に蓄えた水の絵も描いてみます。
水の位置エネルギーの計算式をドラム缶の絵から求めると・・
まずは、底面積:\(S\)のドラム缶に高さ:\(h\)まで水を入れた絵を下に示します。
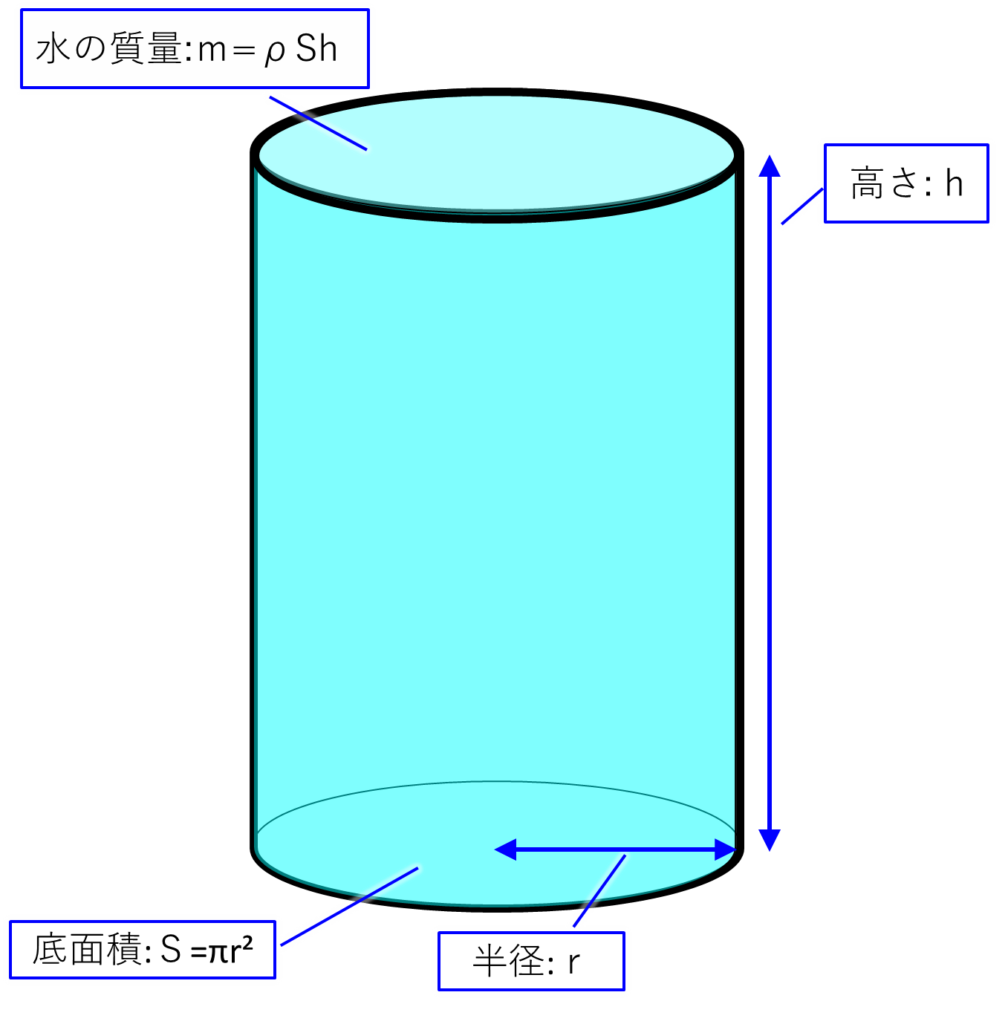
先ほどのグラフと同様、高さ:\(h\)を\(n\)分割します。
\(n\)分割した一番下の水は下の絵のようになります。
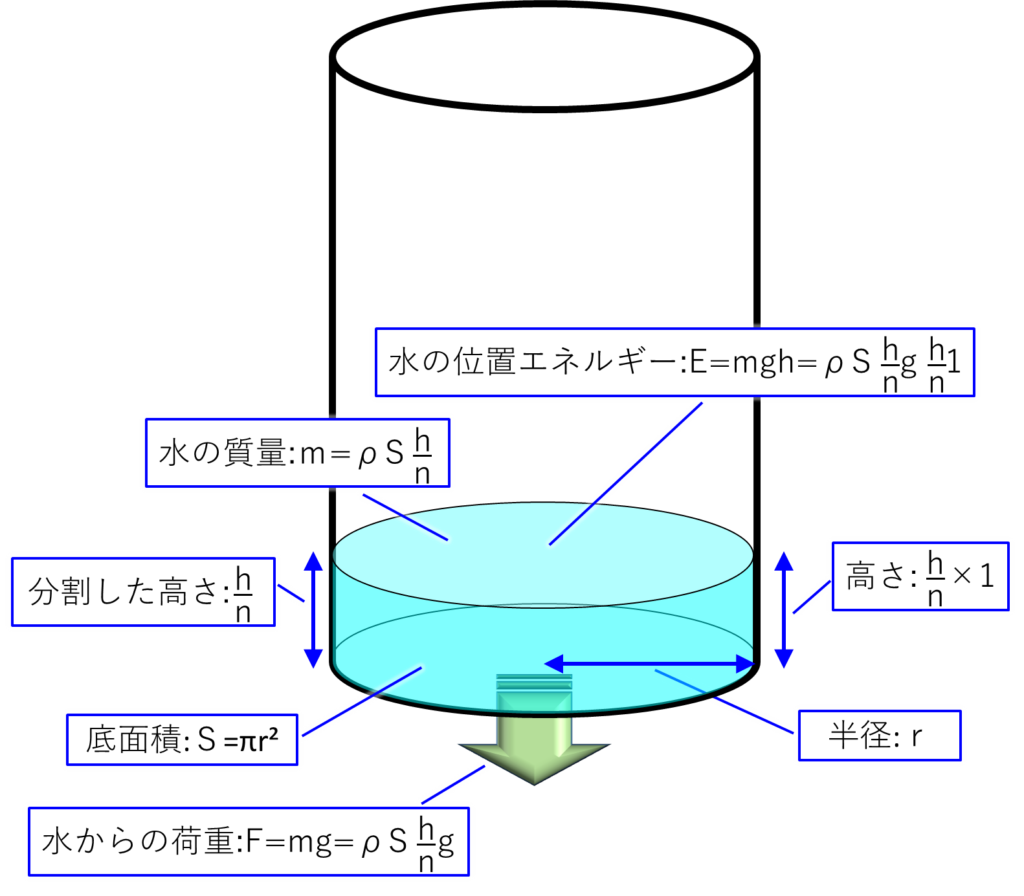
吹き出しをたくさん入れましたが、内容はグラフで書いたものと同じです。
一番下なので、「\(k=1\)」です。
次は、\(n\)分割した二番目の水の絵です。
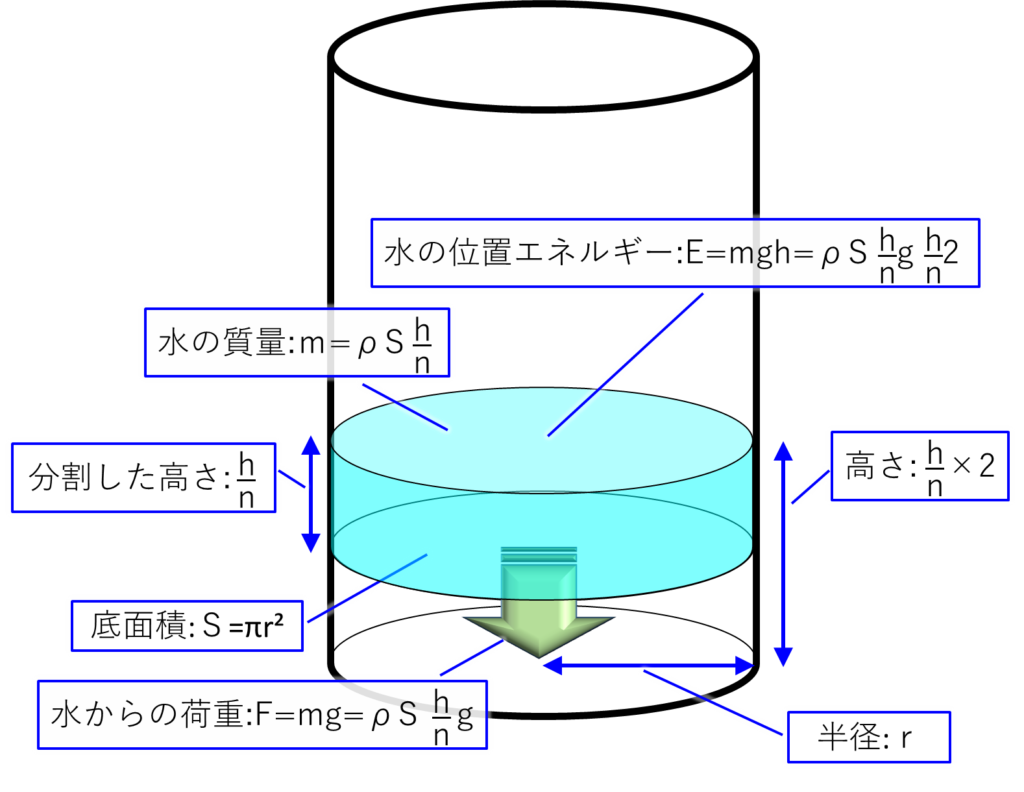
これは2番目なので、「\(k=2\)」です。
次は、\(n\)分割した\(k\)番目の水の絵です。
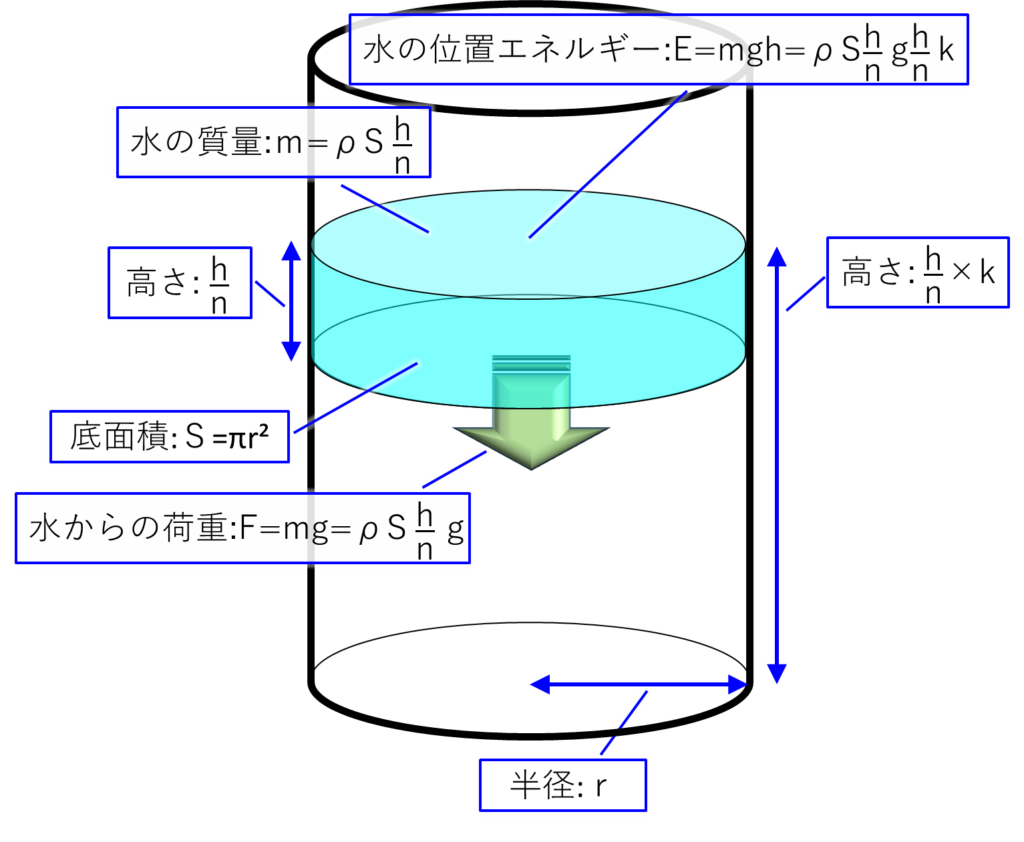
最後に、\(n\)分割した\(n\)番目の水の絵です。
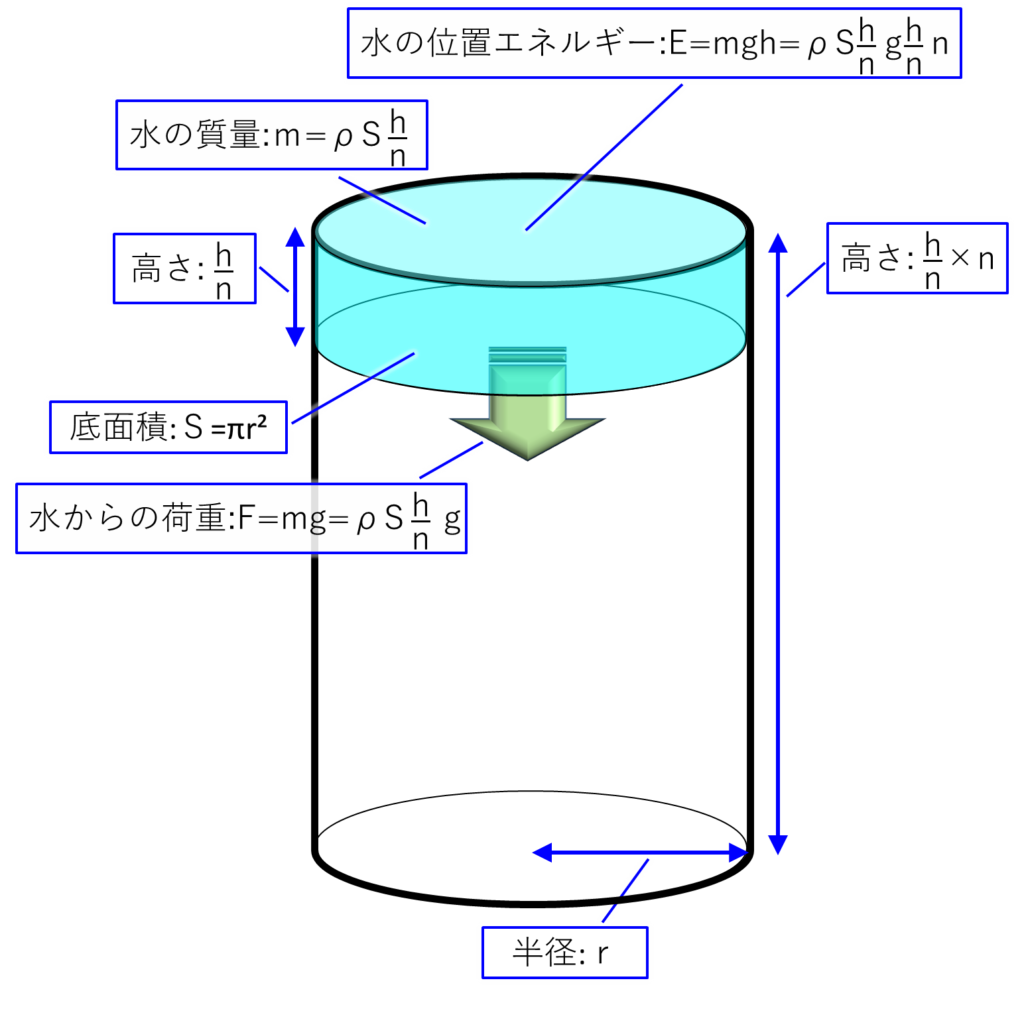
頑張って絵を描いたので、グラフよりも分かりやすくなっているとうれしいです。
さて、それでは先ほどのドラム缶に蓄えた水の位置エネルギーを求める式を解いていきます。
$$E=\lim_{n \to ∞}{\sum_{k=1}^{n} \left(ρS\displaystyle\frac{h}{n}g\right)\left(\displaystyle\frac{h}{n}k\right)}$$
まず、\(ρ,S,h,g\)は分割しても変化しないので、前に出します。
$$E=ρSh^2g\lim_{n \to ∞}{\sum_{k=1}^{n} \left(\displaystyle\frac{1}{n}\right)\left(\displaystyle\frac{1}{n}k\right)}$$
$$=ρSh^2g\lim_{n \to ∞}{\sum_{k=1}^{n} \left(\displaystyle\frac{1}{n}\right)^2k}$$
$$=ρSh^2g\lim_{n \to ∞}\left(\displaystyle\frac{1}{n}\right)^2{\sum_{k=1}^{n} k}$$
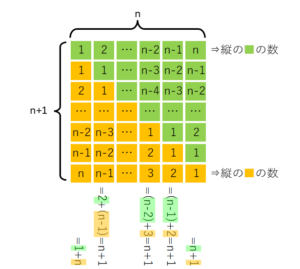
$$=ρSh^2g\lim_{n \to ∞}\left(\displaystyle\frac{1}{n}\right)^2\displaystyle\frac{n(n+1)}{2}$$
$$=ρSh^2g\lim_{n \to ∞}\displaystyle\frac{1}{n^2}\displaystyle\frac{n(n+1)}{2}$$
$$=ρSh^2g\lim_{n \to ∞}\displaystyle\frac{1+\displaystyle\frac{1}{n}}{2}$$
$$=ρSh^2g\displaystyle\frac{1}{2}$$
$$=\displaystyle\frac{1}{2}ρSgh^2$$
水の容器(ドラム缶)は円柱形状なので、水の質量は「\(m=ρSh\)」になるので、これを上の式に入れると下の式になります。
$$E=\displaystyle\frac{1}{2}mgh$$
通常、位置エネルギーの計算式は「\(E=mgh\)」ですが、円柱形状の容器に入れた水の位置エネルギーの計算式は、底面を高さゼロとすると「\(E=\displaystyle\frac{1}{2}mgh\)」になりました。
この考え方を使って、次回はコンデンサーに蓄えられるエネルギーについて書こうと思います。
よろしければ以下のバナーをクリックしていただけると励みになります!
にほんブログ村