微分や積分の話【微分（１）】

今回からは「微分」の話を山の登り下りをイメージしながら書いてみます。

小高い山のイメージ

近所に小高い山があると考えてください。

その山を登って頂上に到着し、そこで引き返さずに反対側に下山するとします。

その山のイメージを下に示します。

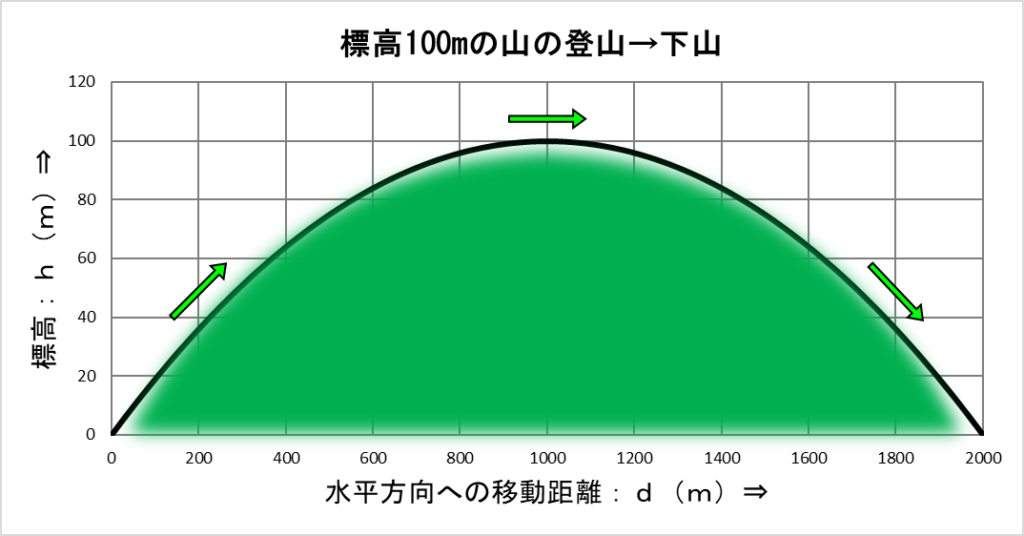
登山口は左下にあって、移動距離：0m、標高：0mの位置です。

そこから右に水平方向に1000m移動すると山の頂上に到着し、標高は100mです。

そのまま右に水平方向に1000m（合計2000m）移動すると下山完了で、標高：0mに戻ります。

この山の登り下りの曲線を、数式で表してみます。

山の登り下りを表す数式

水平方向への移動距離：dから、標高：hを求める式をたてたので下に示します。

$$標高：h=f(d)=100-\displaystyle\frac{(d-1000)^2}{10000}$$

この数式が合っているかを確認するため、この数式の移動距離：dに、いくつかの数字を入れて標高：hを計算してみます。

〔d=0m〕

$$標高：h=f(d)=100-\displaystyle\frac{(0-1000)^2}{10000}=100-\displaystyle\frac{(-1000)^2}{10000}$$

$$=100-\displaystyle\frac{1000000}{10000}=100-100=0$$

これは大丈夫ですね。

〔d=200m〕

$$標高：h=f(d)=100-\displaystyle\frac{(200-1000)^2}{10000}=100-\displaystyle\frac{(-800)^2}{10000}$$

$$=100-\displaystyle\frac{640000}{10000}=100-64=36$$

これも山のイメージ図と見比べると大丈夫そうです。

それではあと、三種類の移動距離についても計算します。

〔d=1000m〕

$$標高：h=f(d)=100-\displaystyle\frac{(1000-1000)^2}{10000}=100-\displaystyle\frac{(0)^2}{10000}$$

$$=100-\displaystyle\frac{0}{10000}=100-0=100$$

〔d=1800m〕

$$標高：h=f(d)=100-\displaystyle\frac{(1800-1000)^2}{10000}=100-\displaystyle\frac{(800)^2}{10000}$$

$$=100-\displaystyle\frac{640000}{10000}=100-64=36$$

〔d=2000m〕

$$標高：h=f(d)=100-\displaystyle\frac{(2000-1000)^2}{10000}=100-\displaystyle\frac{(1000)^2}{10000}$$

$$=100-\displaystyle\frac{1000000}{10000}=100-100=0$$

合計五つの移動距離について標高を計算してみましたが、この数式で大丈夫そうです。

次回の予定

今回は、水平方向への移動距離：dで、標高を計算する数式が分かりました。

次回は、山を登ったり下りたりする時の坂道の傾斜が、水平方向の移動距離でどう変わるのかを書いていきます。

よろしければ以下のバナーをクリックしていただけると励みになります！/

にほんブログ村