微分や積分の話【微分（３）】

2023年1月30日 2023年2月6日

講師Kazu

前回は、山の標高を計算する式から、山の傾斜を計算する式を求めたので、今回はそれと微分の関係を書いてみます。

山の標高と傾斜の関係

これまで、山の登りと下りの話について書いてきました。

最初は山の登山口から、頂上に向かっての登山です。

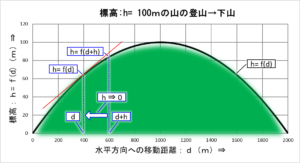
登山中の「標高」と坂道の「傾斜」は、山に登っていくと変化します。

今回の山は、最初は急斜面ですが、山頂に近づくにつれて緩斜面になっていきます。

登山とともに変化する「標高」と「傾斜」を、左下の登山口を基点（0m地点）として、「水平方向の移動距離」から計算する下の計算式を前回と前々回で求めました。

標高：$h=f(d)=100-\displaystyle\frac{(d-1000)^2}{10000}$

傾斜：$s=\displaystyle\frac{1}{5000}(1000-d)$

山頂を過ぎると下り坂になりますが、下りもこの式で計算できます。

この「傾斜」は、微小な「移動」と、それにともなう微小な「標高」の変化の割り算（「標高の変化量」÷「移動の変化量」）で求まるので、下の式になります。

$$s=\lim_{h \to 0}\displaystyle\frac{f(d+h)-f(d)}{(d+h)-(d)}$$

このように、「標高」の計算式から「傾斜」の計算式を導くことが「微分」の一例です。

数学的には正確な表現ではないかもですが・・。

逆に、「傾斜」を計算する式から「標高」を計算する式を導くことは「積分」になります。

これも計算してみましょう。

「傾斜」から「標高」を計算

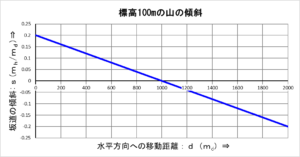
下のグラフは、前回求めた「傾斜」の計算式をグラフ化したものですが、「標高」は「傾斜」に「移動距離」を掛けると計算できます。

「微分や積分の話【積分（２）】」で、「速度」から「走行距離」を計算したときと同じように、今回は「移動距離」を「$\displaystyle\frac{1}{n}$」して計算したのちに、「$n$」を無限大にして「標高」計算していきます。

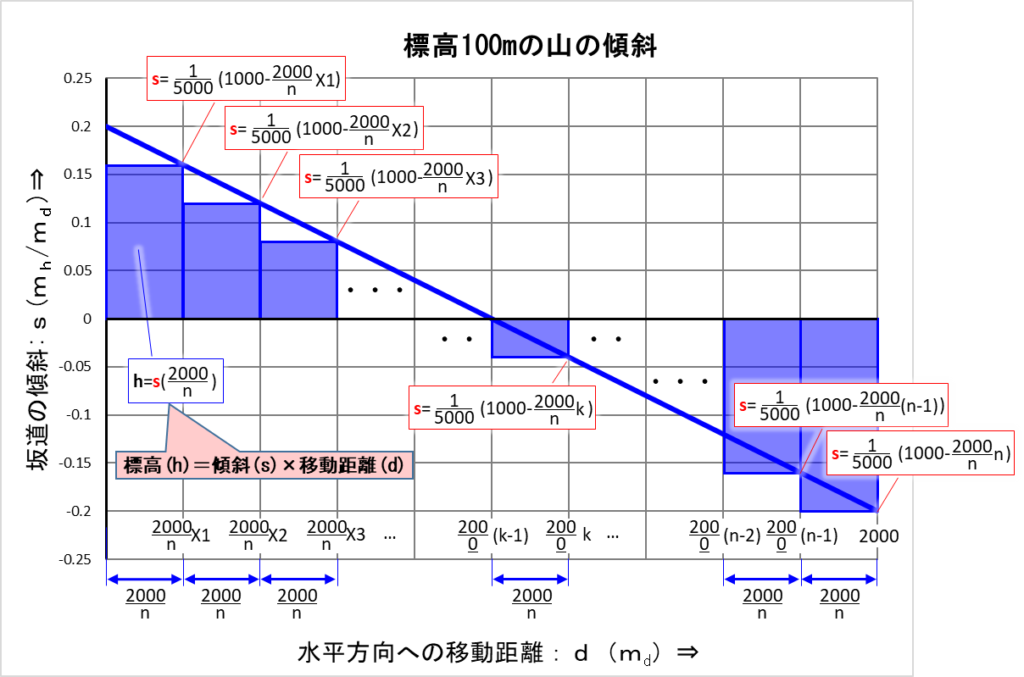
上のグラフを少し説明しておきます。

「水平方向の移動距離」の単位はメートルですが、「標高」と区別するために「水平方向の移動距離」の単位は「$m_d$」、「標高」の単位は「$m_h$」としました。

横軸は「水平方向の移動距離」で、「$0～2000$」$m_d$です。

この「$2000$」$m_d$を「$n$」分割するので、ひと区間は「$\displaystyle\frac{2000}{n}$」$m_d$になります。

そして、その一つひとつの区間の「傾斜：$s$」は、グラフの赤い枠の計算式「$s=\displaystyle\frac{1}{5000}\left(1000-\displaystyle\frac{2000}{n}k\right)$」$m_h/m_d$で求まります。

次に、同じように一つひとつの区間の「標高：$h$」は、青い枠の計算式「$h=s\left(\displaystyle\frac{2000}{n}\right)$」$m_h$で求まります。

今回は「水平方向の移動距離」の「$2000$」$m_d$を一般化して「$d$」$m_d$とします。

そうすると、ひと区間は「$\displaystyle\frac{d}{n}$」$m_d$、赤い枠の計算式は「$s=\displaystyle\frac{1}{5000}\left(1000-\displaystyle\frac{d}{n}k\right)$」$m_h/m_d$、青い枠の計算式は「$h=s\left(\displaystyle\frac{d}{n}\right)$」$m_h$になります。

それでは「水平方向の移動距離：$d$」$m_d$から「標高：$h$」$m_h$を計算する式を立てます。

$$h=\lim_{n \to ∞}{\sum_{k=1}^{n} \displaystyle\frac{1}{5000}\left(1000-\displaystyle\frac{d}{n}k\right)}\left(\displaystyle\frac{d}{n}\right)$$

$$=\displaystyle\frac{1}{5000}\lim_{n \to ∞}\sum_{k=1}^{n} \left(1000\left(\displaystyle\frac{d}{n}\right)-k\left(\displaystyle\frac{d}{n}\right)^2\right)$$

$$=\displaystyle\frac{1}{5000}\lim_{n \to ∞} \left( \left(1000\left(\displaystyle\frac{d}{n}\right)-1\left(\displaystyle\frac{d}{n}\right)^2\right)+\left(1000\left(\displaystyle\frac{d}{n}\right)-2\left(\displaystyle\frac{d}{n}\right)^2\right)+・・+\left(1000\left(\displaystyle\frac{d}{n}\right)-n\left(\displaystyle\frac{d}{n}\right)^2\right)\right)$$

$$=\displaystyle\frac{1}{5000}\lim_{n \to ∞}\left(\left(1000\left(\displaystyle\frac{d}{n}\right)+1000\left(\displaystyle\frac{d}{n}\right)+・・+1000\left(\displaystyle\frac{d}{n}\right)\right)-\left(1\left(\displaystyle\frac{d}{n}\right)^2+2\left(\displaystyle\frac{d}{n}\right)^2+・・+n\left(\displaystyle\frac{d}{n}\right)^2\right)\right)$$

$$=\displaystyle\frac{1}{5000}\lim_{n \to ∞}\left(\left(1000\left(\displaystyle\frac{d}{n}\right)×n\right)-\left(\left(1+2+・・+n\right)\left(\displaystyle\frac{d}{n}\right)^2\right)\right)$$

$$=\displaystyle\frac{1}{5000}\lim_{n \to ∞}\left(\left(1000d\right)-\left(\left(\displaystyle\frac{n(n+1)}{2}\right)\left(\displaystyle\frac{d}{n}\right)^2\right)\right)$$

$$=\displaystyle\frac{1}{5000}\lim_{n \to ∞}\left(1000d-\displaystyle\frac{1(1+\displaystyle\frac{1}{n})}{2}d^2\right)$$

$$=\displaystyle\frac{1}{5000}\left(1000d-\displaystyle\frac{1(1+0)}{2}d^2\right)$$

$$=\displaystyle\frac{1}{5000}\left(1000d-\displaystyle\frac{1}{2}d^2\right)$$

$$=\displaystyle\frac{1}{5}d-\displaystyle\frac{1}{10000}d^2$$

今回は説明を省略しましたが、計算の途中に「微分や積分の話【積分（１）】」の「1からnまでの和を求める公式」を使用しました。

「$1+2+3+・・・+n=\displaystyle\frac{n(n+1)}{2}$」という公式です。

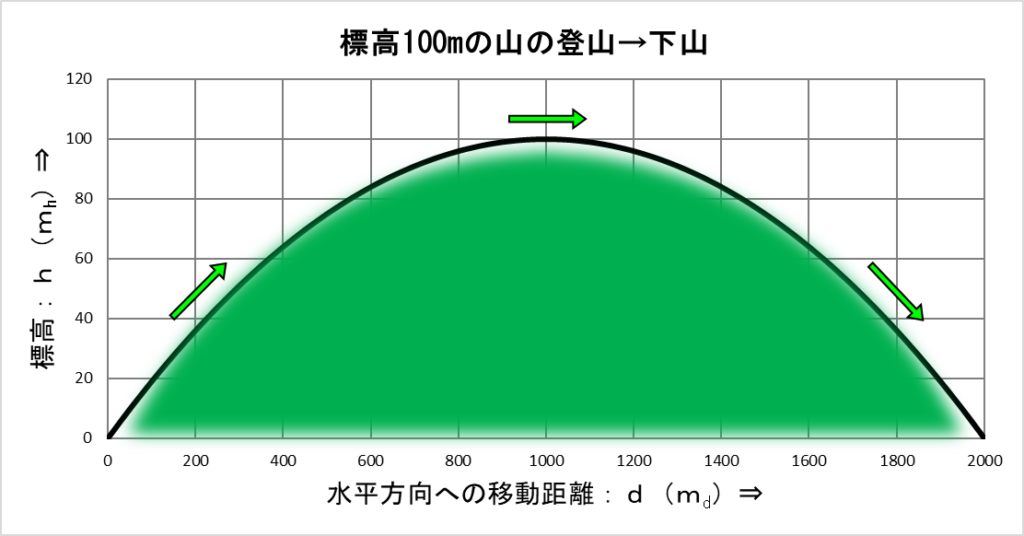
ここで求めた式を使って「水平方向への移動距離：$d$」を横軸、「標高：$h$」を縦軸にしてグラフを書くと下のようになります。

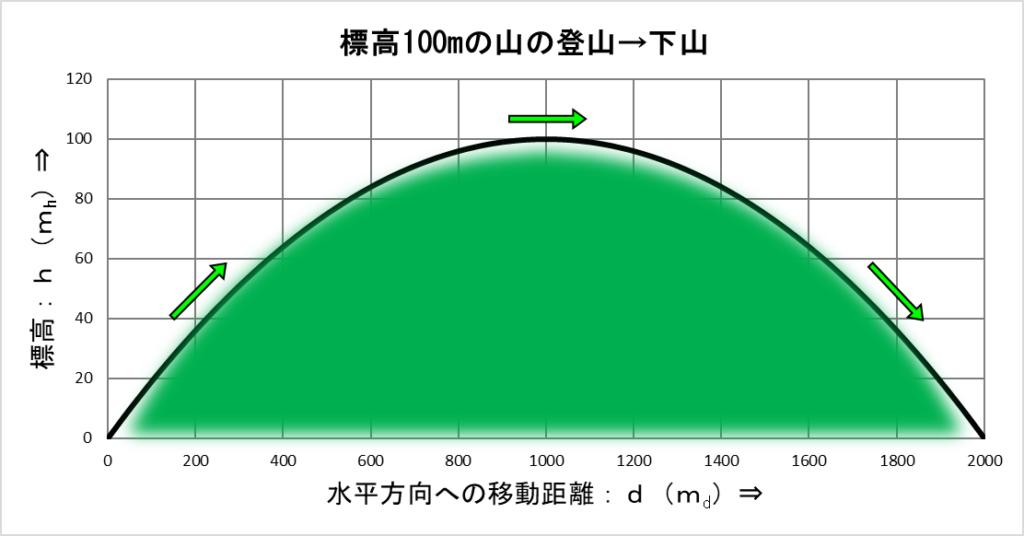
これは、最初の山の形と同じです。

「水平方向への移動距離：$d$」から「標高：$h$」を求める計算式を微分すると「傾斜：$s$」が求まりました。

その「傾斜：$s$」を求める計算式を積分すると「標高：$h$」を求める計算式が求まりました。

積分で求めた$\left(h=\displaystyle\frac{1}{5}d-\displaystyle\frac{1}{10000}d^2\right)$の計算式と、最初の$h=100-\displaystyle\frac{(d-1000)^2}{10000}$の計算式は一見、別の計算式に見えるので、最初の式を変形して同じ式かを確認してみます。

$$h=100-\displaystyle\frac{(d-1000)^2}{10000}$$

$$=100-\displaystyle\frac{d^2-2×1000d+1000000}{10000}$$

$$=100-\left(\displaystyle\frac{1}{10000}d^2-\displaystyle\frac{2}{10}d+100\right)$$

$$=\displaystyle\frac{1}{5}d-\displaystyle\frac{1}{10000}d^2$$

二つの標高を求める式は、同じ計算式であることが確認できました。