微分や積分の話【まとめ】

2023年2月6日 2023年2月7日

講師Kazu

コンデンサーやコイルの話を書くのに必要と思い、微分や積分の話を書きましたが、最後にまとめてみます。

【微分】の説明では、山の標高と傾斜について書いてきました。

下のグラフでは、横軸が「水平方向への移動距離」、縦軸が「標高」です。

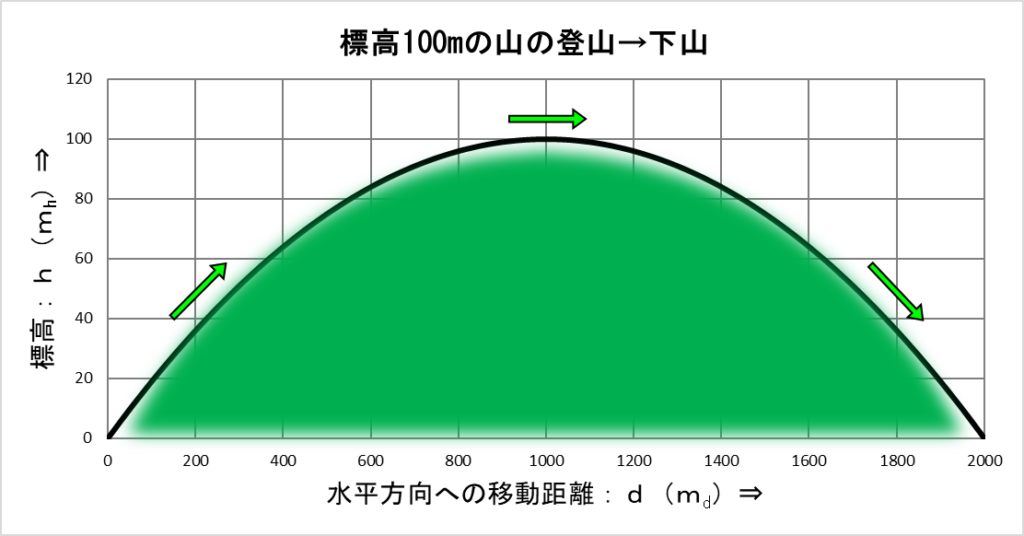
この関係を表す式は下記でした。

標高：\(h=100-\displaystyle\frac{(d-1000)^2}{10000}=-\displaystyle\frac{1}{10000}d^2+\displaystyle\frac{1}{5}d\)

この式を「微分や積分の話【微分（３）】」に書いた「微分の公式」を使って微分すると下記になります。

標高を微分：\(h'=\displaystyle\frac{dh}{dd}=-\displaystyle\frac{2}{10000}d+\displaystyle\frac{1}{5}=s\)

「\(\displaystyle\frac{dh}{dd}\)」は「\(h\)」を「\(d\)」で微分することを表す記号です。

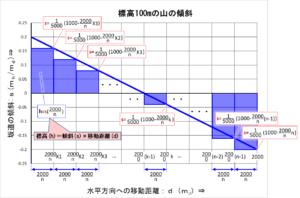
標高を微分した式のグラフは下記ですが、縦軸は山の傾斜：\(s\)です。

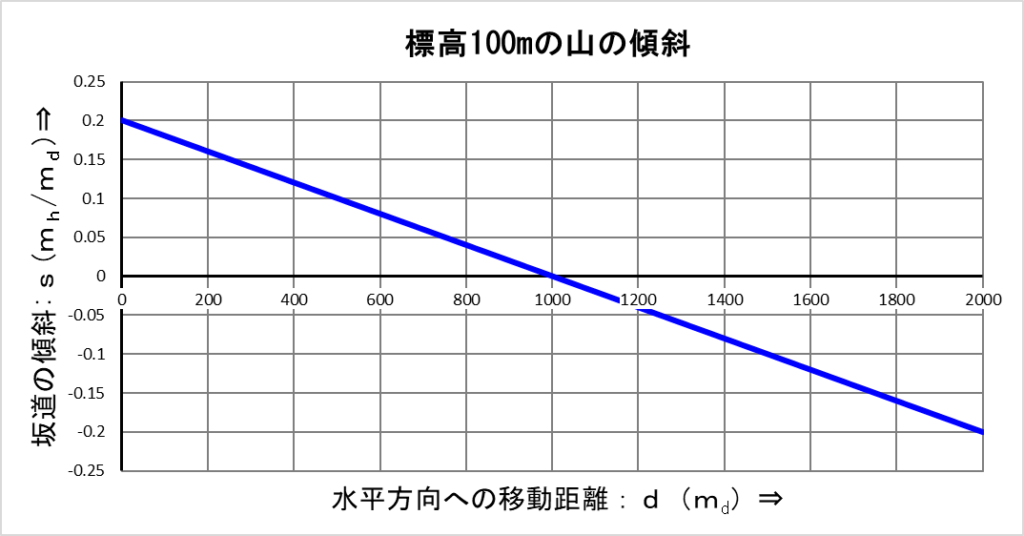
この傾斜の式を逆に、「微分や積分の話【積分（３）】」に書いた「積分の公式」を使って積分すると下記になります。

傾斜を積分：\(\int{s}dd=\int{(-\displaystyle\frac{2}{10000}d+\displaystyle\frac{1}{5})}dd=-\displaystyle\frac{1}{10000}d^2+\displaystyle\frac{1}{5}d\)

傾斜を積分して求めた式をグラフ化すると、元の標高を表すグラフになります。

積分すると、通常は求めた式の後ろに「\(+C\)」という積分定数が付きますが、今回は積分した結果が「\(d=0\)」のときに「\(h=0\)」としたので「\(C=0\)」となります。

【積分】の説明では、飛行機の加速度と速度と走行距離について書きました。

加速度を「\(a\)」、速度を「\(v\)」、走行距離を「\(s\)」としています。

まず最初に、横軸時間「\(t\)」で加速度「\(a\)」としたグラフを下に示します。

加速度は時間に対して一定の値としました。

加速度：\(a\)

加速度に時間をかけると速度になりますので、積分すると速度が求まります。

加速度を時間で積分：\(\int{a}dt=v=at\)

この「\(v=at\)」をグラフ化すると下記になります。

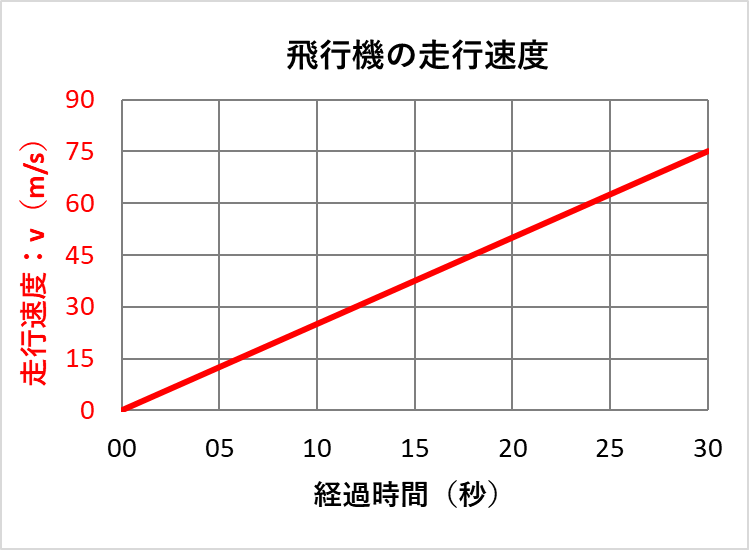
今回も「\(t=0\)」のときに「\(v=0\)」としたので積分定数は「\(C=0\)」となります。

速度「\(v\)」に時間をかけると走行距離になりますので、積分すると走行距離が求まります。

速度を時間で積分：\(\int{v}dt=s=\int{at}dt=\displaystyle\frac{1}{2}at^2\)

この「\(s=\displaystyle\frac{1}{2}at^2\)」をグラフ化すると下記になります。

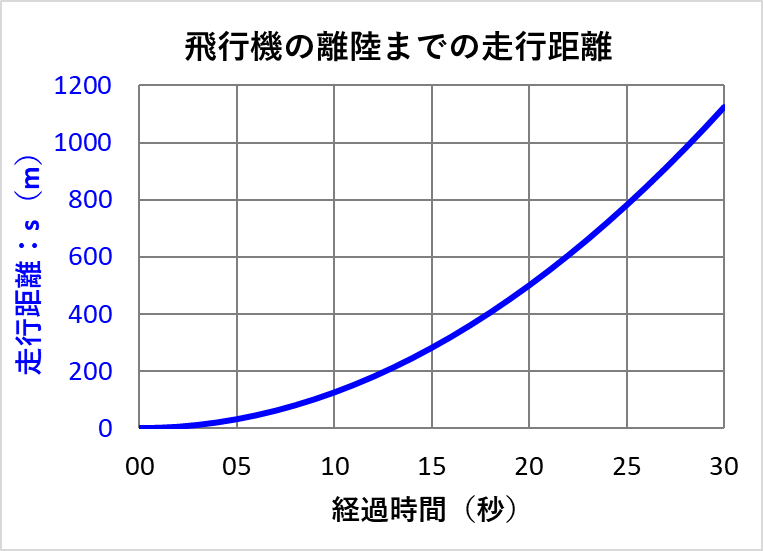
ここでも、「\(t=0\)」のときに「\(s=0\)」としたので積分定数は「\(C=0\)」となります。

逆に「\(s=\displaystyle\frac{1}{2}at^2\)」を時間で微分すると、走行距離のグラフの傾斜が求まり、それが速度になります。

さらに「\(v=at\)」を時間で微分すると、速度のグラフの傾斜が求まり、それが加速度になります。

この微分の計算は省略しますので、「微分や積分の話【微分（３）】」の最後に書いた「微分の公式」を使って求めてみてください。

今回は、これまで書いてきた微分と積分について、微分と積分の公式を一通り振り返ってみました。

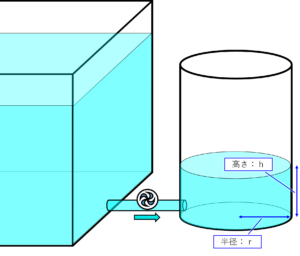
次回は応用編として、ドラム缶のような円柱状の容器に水を下から入れたときのイメージで、水の位置エネルギーを計算してみようと思います。

それが終わったら、再びコンデンサーやコイルの話に戻ろうと思います。

よろしければ以下のバナーをクリックしていただけると励みになります！