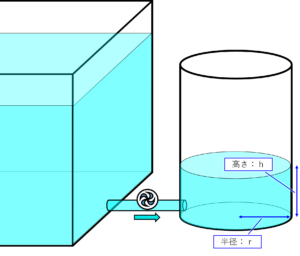
「1からｎ（自然数）までの和」の公式をもう一度

2023年2月27日 2023年10月28日

講師Kazu

【積分（１）】の投稿で上の題名の内容を書きましたが、もう少し分かりやすい公式の導き方を思いついたので書いておきます。

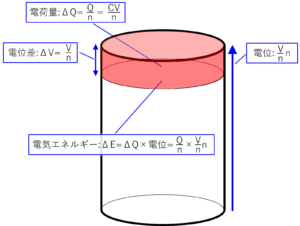
前回の投稿の最後に「次回はコンデンサー」と書きましたが、今回はこのネタを書かせてください。

前回の「ドラム缶」の投稿でも使用した下の公式の求め方です。

$$\sum_{k=1}^{n} k=1+2+ … +(n-1)+n=\displaystyle\frac{n(n+1)}{2}$$

【積分（１）】の投稿では、自分が分かりやすいと思った内容を書きましたが、見直してみるとそうでもないように思ったので、もう一度書きます。

【積分（１）】の投稿では下の図を使って説明しました。

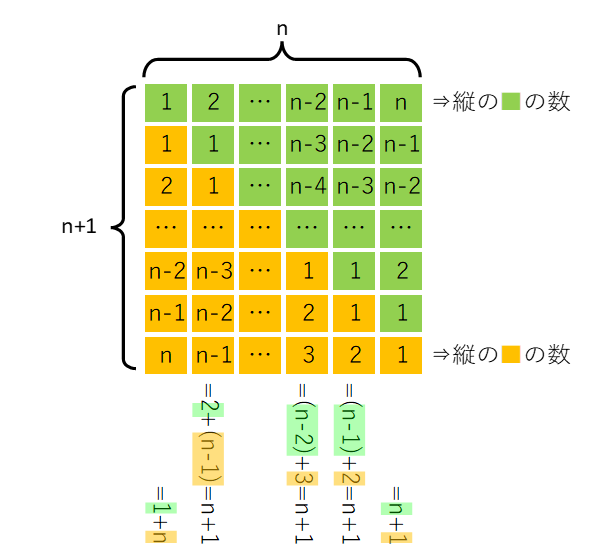
「$1+2+ … +n$」の「$1$」「$2$」…「$n$」の数を■の個数で表せば、視覚的に$（n+1）$が$n$個のあることが理解しやすいのではと思いましたが、あとで見ると分かりづらく感じました。

試行錯誤になりますが、今回は絵ではなく二つの計算式の両辺を足し合わせます。

その計算式は下になります。

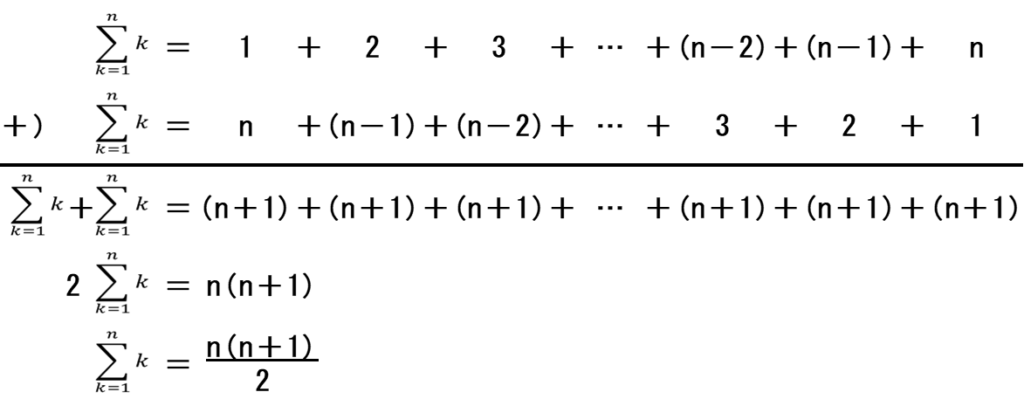
横線の上の二つの計算式は基本的に同じで、上の式の右辺は右にいくほど数値が増え、下の式の右辺は右にいくほど数値が小さくなるように並べています。

この二つの計算式を足すと、横線の下の計算式になります。

横線の下の計算式は、右辺に$（n+1）$が$n$個あるので「$n(n+1)$」になり、左辺に「$\sum k$」が$2$個あるので「$2\sum k$」になります。

この両辺を「$2$」で割ると「$\sum k$」が「$\displaystyle\frac{n(n+1)}{2}$」になります。

こちらの方が、分かりやすいと今は感じています。

次回こそは「コンデンサー」の話を書こうと思います。

よろしければ以下のバナーをクリックしていただけると励みになります！