微分や積分の話【微分（２）】

今回は、山の登り下りをするときの傾斜を計算で求めます。

前回の小高い山のイメージ

前回は、下に示す小高い山をイメージしました。

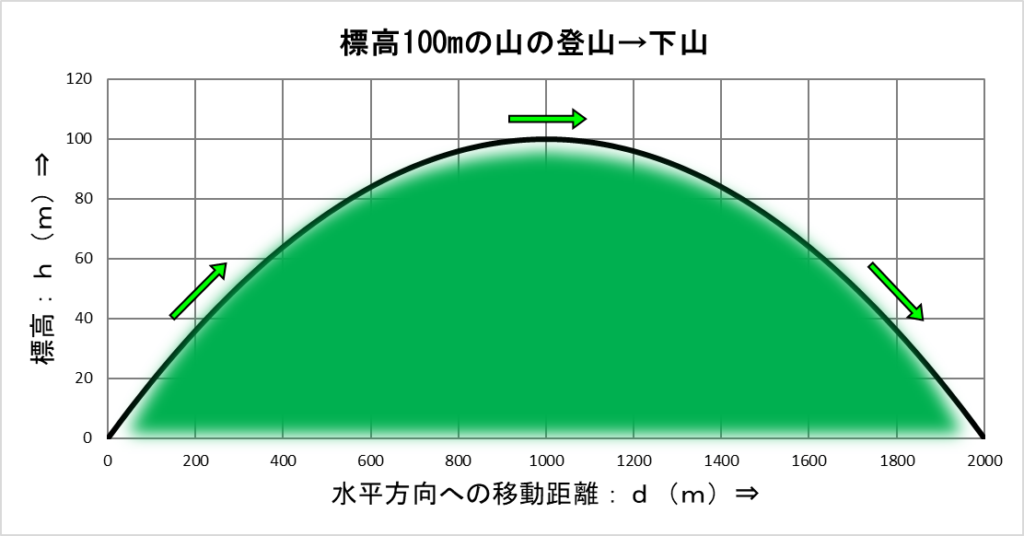
この山の左端から登山を始めて、山の頂上に着いたらそのまま反対側に向かって下山することにします。

このときの標高：h は、移動距離：d を使って下の式で計算できます。

$$標高：h=f(d)=100-\displaystyle\frac{(d-1000)^2}{10000}$$

上の式の「\(f(d)\)」は関数を表す記号で、変化する数：\(d\)を使って計算する式を表します。

今回はこの式から、登り下りの坂道の傾斜：s を移動距離：d を使って表す式を求めます。

小高い山の登り下りの傾斜

小高い山の登り下りの傾斜を計算するために、下の図に示すように移動距離：d と、そこから少し移動した距離：d+h の間の高低差から傾斜を計算します。

上の図の赤い線の傾斜は、移動距離：d ～ d+h までの間の傾斜です。

今、計算したいのは移動距離：d での傾斜なので、h を0に近づけます。

その様子を下の図に示します。

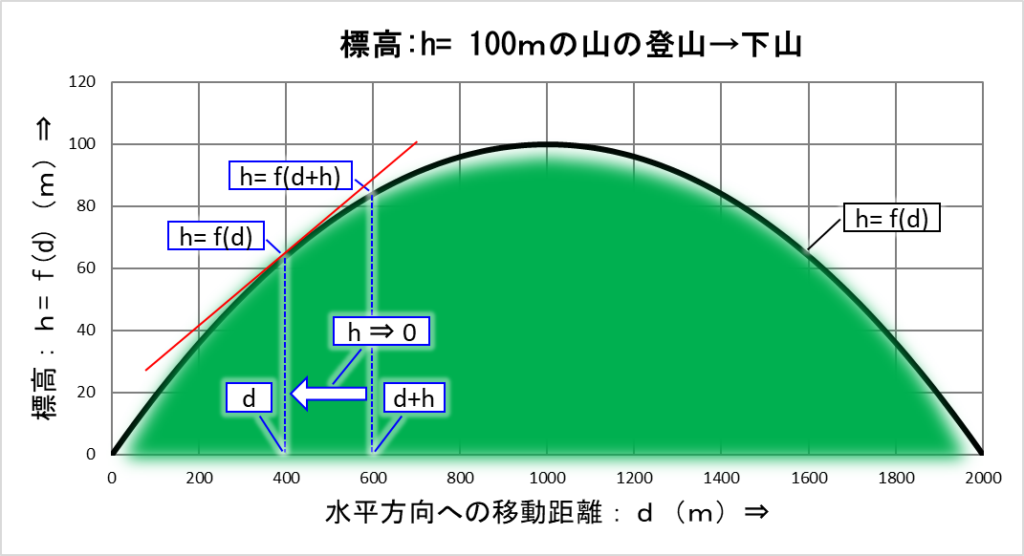
この赤い線の傾斜を計算するれば、移動距離：d での傾斜が求まりそうです。

この赤い線の傾斜を求める式を書くと、下記になります。

$$移動距離：dでの坂道の傾斜：s=\lim_{h \to 0}\displaystyle\frac{f(d+h)-f(d)}{(d+h)-(d)}$$

傾斜なので、標高を分数の分子、移動距離を分母にして、hをゼロに近づけるという式です。

それでは、この式を解いていきます。

少し長いのですが、計算は基本的に四則計算なので追っかけてみてください。

$$s=\lim_{h \to 0}\displaystyle\frac{f(d+h)-f(d)}{(d+h)-(d)}$$

$$=\lim_{h \to 0}\displaystyle\frac{\left(100-\displaystyle\frac{((d+h)-1000)^2}{10000}\right)-\left(100-\displaystyle\frac{(d-1000)^2}{10000}\right)}{h}$$

$$=\lim_{h \to 0}\displaystyle\frac{(100-100)+\displaystyle\frac{(d-1000)^2}{10000}-\displaystyle\frac{((d+h)-1000)^2}{10000}}{h}$$

$$=\lim_{h \to 0}\displaystyle\frac{\displaystyle\frac{(d-1000)^2-((d+h)-1000)^2}{10000}}{h}$$

$$=\lim_{h \to 0}\displaystyle\frac{(d^2-2000d+(-1000)^2)-((d+h)^2-2000(d+h)+(-1000)^2)}{10000h}$$

$$=\lim_{h \to 0}\displaystyle\frac{(d^2-2000d)-(d^2+2hd+h^2-2000d-2000h))}{10000h}$$

$$=\lim_{h \to 0}\displaystyle\frac{(d^2-2000d)-((d^2-2000d)+2hd+h^2-2000h))}{10000h}$$

$$=\lim_{h \to 0}\displaystyle\frac{2000h-2hd-h^2}{10000h}$$

$$=\lim_{h \to 0}\displaystyle\frac{2000-2d-h}{10000}$$

$$=\displaystyle\frac{2000-2d}{10000}$$

$$=\displaystyle\frac{1}{5000}(1000-d)$$

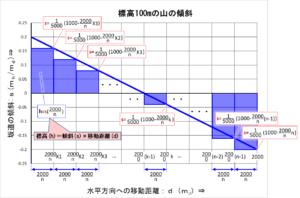
この式でグラフを作成すると下記になります。

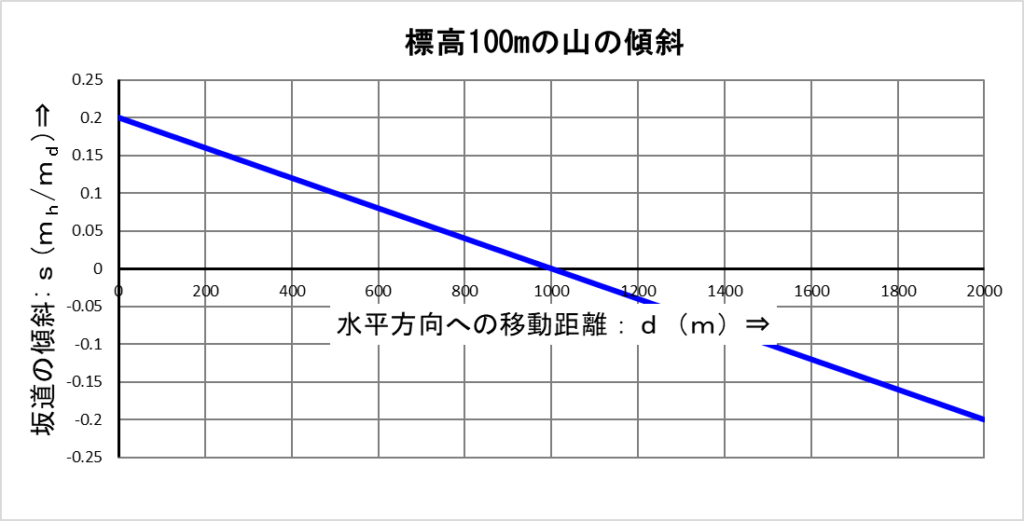
縦軸の傾斜の単位は「\(m_h/m_d\)」としていますが、分子の標高の単位を「\(m_h\)」、分母の移動距離の単位を「\(m_d\)」としました。

移動距離：d=0(\(m_d\)) での傾斜は0.2(\(m_h/m_d\)) で、1(\(m_d\)) 進むと標高が0.2(\(m_h\)) 上がることを示しています。

移動距離：d=1000(\(m_d\)) での傾斜は0.0(\(m_h/m_d\)) で平坦となり、移動距離：d=2000(\(m_d\)) での傾斜は-0.2(\(m_h/m_d\)) で、1(\(m_d\)) 進むと標高が0.2(\(m_h\)) 下がることを示しています。

これで、移動距離：d から坂道の傾斜：s を計算する式を求めることができました。

微分との関係について

今回もちょっと、時間が無くなってしまいました。

微分との関係などは次回書こうと思います。

よろしければ以下のバナーをクリックしていただけると励みになります！

にほんブログ村