直流と交流の違い〔８〕（交流電源１周期分のエネルギーの計算式）

前回は「経過時間：\(t\) 」での、瞬間的な「消費電力：\(P_{AC} (t)\) 」を計算する式を求めたので、ここからはこの式で計算した瞬間、瞬間の電力に時間を掛けて、瞬間、瞬間の電力量を計算します。

次に、それらを全て足し合わせて全体の電力量を計算し、それを時間で割り算して消費電力の平均値を計算する式を求めます。

交流電源の電圧と電力のおさらい

おさらいもかねて、これまでと同様のグラフを下に示します。

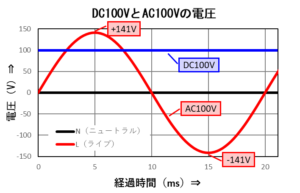
まずは、「家庭用交流電源：AC100V」の電圧の変化の様子を示すグラフです。

縦軸は具体的な電圧値ではなく、赤い線が時間の経過でどう変化するかを表す式にしました。

周波数は50Hzとしているので、20ms周期の繰り返し波形になります。

「\(\omega t\)」は角周波数と経過時間を掛けたもので、単位は「rad（ラジアン）」です。

この辺りは、これまで書いてきた通りです。

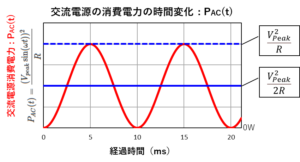
この交流電源に「抵抗：\(R\) 」を接続したとき、「抵抗：\(R\) 」で消費する電力は下のグラフのようになります。

電圧のトレースは20ms周期でしたが、消費電力のトレースは10ms周期になっているので、20msだと2周期です。

また、電圧のグラフは0Vを挟んでプラス側とマイナス側に上下していましたが、消費電力のグラフは、0Wから上の方で上下しています。

平均化した消費電力を求める計算式

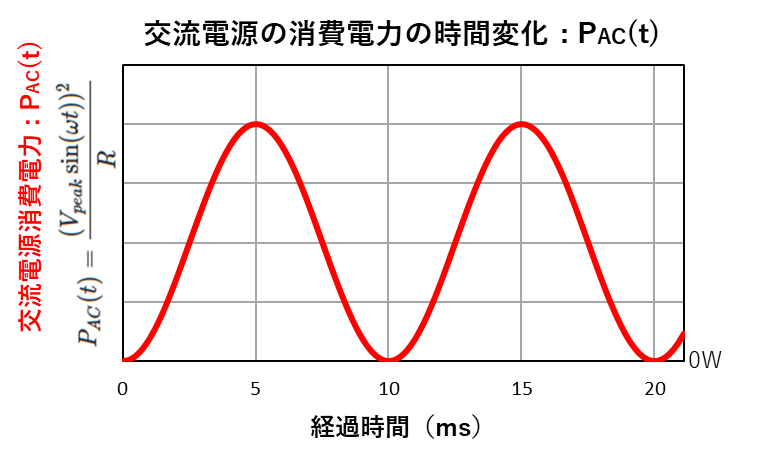
それでは最初に書いたように、「消費電力：\(P_{AC} (t)\) 」の瞬間、瞬間の電力をイメージしたグラフを下に示します。

これまで何度も使ってきた方法ですが、横軸の「経過時間」をn分割します。

そうすると、分割された一つひとつの長方形は消費電力と時間の掛け算なので、この長方形の面積は電力量になります。

電力量の単位は、「W・s（ワット・セカンド）＝ J（ジュール）」です。

「0ms」から「20ms」までの一周期の消費電力の平均値は、「0ms」から「20ms」までを合計した電力量（赤色の面積）を、経過時間の「20ms」で割り算すれば求まります。

それでは、一周期：20msを「\(T\) 」として計算していきます。

「\(T\) 」をn分割した１番目の経過時間は下の式で表せます。

$$t_1=1 ✕ \displaystyle\frac{T}{n} $$

同様にして２番目、k番目、n番目の経過時間の式を下に示します。

$$t_2=2 ✕ \displaystyle\frac{T}{n} $$

$$t_k=k \displaystyle\frac{T}{n} $$

$$t_n=n \displaystyle\frac{T}{n} $$

次に、n分割した一つ目の長方形の電力量「\(E_1\) 」は下の式で表せます。

$$E_1= \displaystyle\frac{(V_ {peak} \sin (\omega t_1))^{2}}{R} ✕ \displaystyle\frac{T}{n} $$

$$= \displaystyle\frac{\left(V_ {peak} \sin \left(\omega \displaystyle\frac{T}{n} \right) \right)^{2}}{R} ✕ \displaystyle\frac{T}{n} $$

同様にして２番目、k番目、n番目の電力量の式を下に示します。

$$E_2= \displaystyle\frac{\left(V_ {peak} \sin \left(\omega \displaystyle\frac{2T}{n} \right) \right)^{2}}{R} ✕ \displaystyle\frac{T}{n} $$

$$E_k= \displaystyle\frac{\left(V_ {peak} \sin \left(\omega \displaystyle\frac{kT}{n} \right) \right)^{2}}{R} ✕ \displaystyle\frac{T}{n} $$

$$E_n= \displaystyle\frac{\left(V_ {peak} \sin \left(\omega \displaystyle\frac{nT}{n} \right) \right)^{2}}{R} ✕ \displaystyle\frac{T}{n} $$

「\(E_1\) 」から「\(E_n\) 」まで足し算した「\(E\)」の式は、下記になります。

$$E=\lim_{n \to ∞}\sum_{k=1}^{n} \left(\displaystyle\frac{\left(V_ {peak} \sin \left(\omega \displaystyle\frac{kT}{n} \right) \right)^{2}}{R} ✕ \displaystyle\frac{T}{n} \right)$$

この式を解いて、「\(T\) 」で割り算すれば消費電力が求まるはずです。

これをまともに計算するのは自分には難しいと思うので、次回は小技を使いながら計算してみます。

よろしければ以下のバナーをクリックしていただけると励みになります！

にほんブログ村


人気ブログランキング