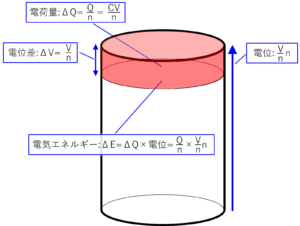
電気回路_コンデンサーのエネルギー〔２〕

2023年3月27日 2023年3月27日

講師Kazu

前回の投稿で「水槽の中の水」と「コンデンサーの中の電荷」が似ていると書きましたが、今回は「位置エネルギー」と「静電エネルギー」の共通点をもう少し掘り下げてみます。

地上の「重力場」で1kgの質量の重りを手に乗せると9.8Nの力が手に加わりますが、それと同様に「電場」に「電荷」を置くと「電荷」に力が加わります。

「電場」と同じ意味の言葉に「電界」があり、自分は普段「電界」という言葉を使うので「電界」で記事を書きます。

「電界」を下の図で説明します。

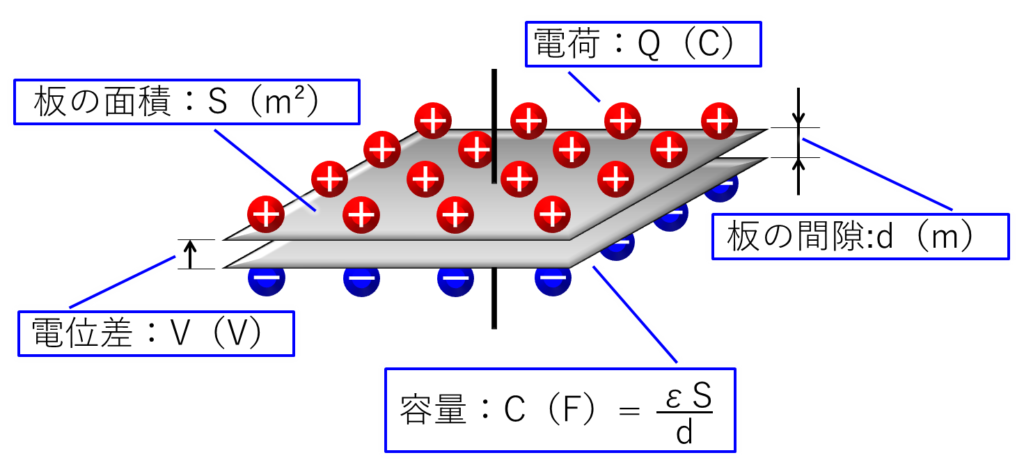
この絵にはいろいろ詰め込んだので、「電界」の説明に使用するところだけを抜き出した絵を下に示します。

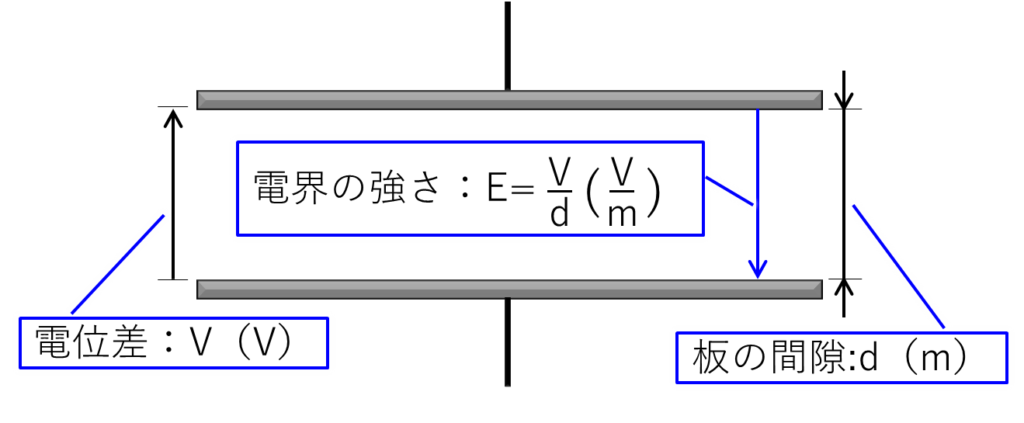
この絵は、上の絵の2枚の板を横から見た絵です。

2枚の板の間に電位差があると、その2枚の板の間には「電界」が発生します。

2枚の板の間には「＋」から「－」に向かって「電気力線」が伸びていると考えます。

「磁界」で「N極」から「S極」に伸びる「磁力線」と同じイメージです。

2枚の板の間には「Ｖ（V）」の電位差があるので、下の板の電位を「0（V）」とすると、上の板の電位は「Ｖ（V）」で、2枚の板の間の電位は下の図の右に描いたグラフに示すように、上の板に近づくほど電位は「Ｖ（V）」に近づきます。

右に描いたグラフの縦軸は下の板からの距離で、横軸はその位置での電位です。

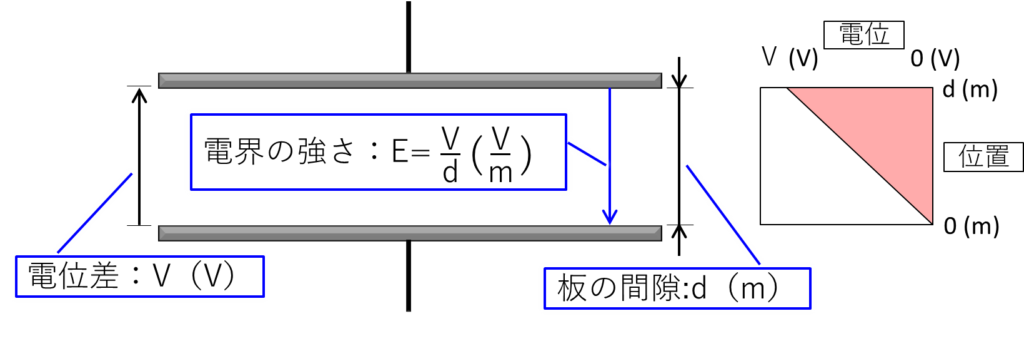
この右のグラフの傾斜が「電界の強さ」や「電界強度」とよばれ、「$E=\displaystyle\frac{V}{d}$」で計算できて単位は「$\displaystyle\frac{V}{m}$」です。

それでは、「電界」に「電荷」を置いたときに「電荷」が受ける力を計算します。

「電界」で「電荷」が受ける力は、「電界」と「電荷」の掛け算で求まります。

力を「$F$」、電荷を「$Q$」、電界の強さを「$E$」とすると計算式は下記になります。

$$F=QE$$

力の単位はニュートン：$N=kg・m/s^2$なので、$1V/m$の強さの電界中に置いた$1C$の電荷には$1N$の力が加わります。

この電荷に加わる力から、静電エネルギーを求めてみます。

前回の投稿で、１ジュール（Ｊ）の仕事の「位置エネルギーの定義」を下のように書きました。

「１ニュートンの力がその力の方向に物体を１メートル動かすときの仕事」

この定義から、仕事（エネルギー）の計算式は、力を「$F$」、移動距離を「$d$」とすると下記になります。

$$仕事=Fd$$

この式に$F=QE$を入れて計算していきます。

$$仕事=Fd=QEd=Q\displaystyle\frac{V}{d}d=QV$$

この計算の結果は、前回使用した$静電エネルギー=QV$と同じ式です。

前回の投稿では、仕事（エネルギー）を表す記号に「$E$」を使用しましたが、今回は電界の強さに「$E$」を使用したので「仕事」としています。

今回は、「電荷に加わる力」と「位置エネルギー」の考え方から「静電エネルギー」の式を求めました。

次回は、これに関連する話をもう少し続けたいと思います。

よろしければ以下のバナーをクリックしていただけると励みになります！