直流と交流の違い〔７〕（電源に接続した抵抗：100Ωでの消費電力）

書いている目的を忘れそうになりますが、「直流と交流の違い〔２〕」で書いたように、AC100Vの変化がどうして「+141V」から「-141V」なのかを書いていきます。

DC100VとAC100Vの電圧のおさらい

ここで、もう一度直流のDC100Vと、交流のAC100Vの波形を載せておきます。

この波形の青い線が直流のDC100Vで、常に100V一定の電圧です。

黒い線はGND（グランド）で、こちらは0V一定です。

一方の赤い波線はAC100Vで、「+141V」から「-141V」くらいまで電圧が変化しています。

AC100Vについてもう少し具体的に書くと、下の画像に示す壁のコンセントの左側がグラフの黒いGND線で、右側が赤い波線になります。

右側と左側で、プラグを差し込む幅が異なっていますので、ご自宅のコンセントを確認してみてください。

DC100VとAC100Vに接続した抵抗の消費電力

直流のDC100Vに、抵抗：Rを接続した回路図を下に示します。

赤い矢印は、流れる電流の向きです。

このとき、「抵抗：\(R\) 」で消費する「電力：\(P_{DC}\) 」は下の式で求めることができます。

$$P_{DC}=V_{DC} I=V_{DC} \displaystyle\frac{V_{DC}}{R} =\displaystyle\frac{(V_{DC})^{2}}{R}$$

次に交流のAC100Vに、「抵抗：\(R\) 」を接続した回路図を下に示します。

赤い矢印が上方向と下方向があるのは、VACの「L」の電圧が、「N」に対してプラス側になったりマイナス側になったりして、電流の流れる向きが変わるためです。

同様に、この「抵抗：\(R\) 」で消費する「電力：\(P_{AC}\) 」は下の式で求まります。

$$P_{AC}=V_{AC} I=V_{AC} \displaystyle\frac{V_{AC}}{R} =\displaystyle\frac{(V_{AC})^{2}}{R}$$

イメージとしてはこのような式になりますが、交流電圧「\(V_{AC}\) 」は時間とともに変化するのでこれを「\(V_{AC}(t)\) 」とし、「時間：\(t\) 」で表す式にしました。

$$V_{AC}(t)=V_ {peak} \sin (\omega t) $$

「\(V_{peak}\)」や「\(\sin (\omega t) \)」は前回までの投稿で説明した内容で、下のグラフのようになります。

横軸の「0～20」は経過時間で単位は「ms」です。

この「経過時間：\(t\)」（単位はs）と「角周波数：\(\omega\)」（単位はrad/s）をかけると単位が「rad（ラジアン）」の角度になります。

この「\(V_{AC}(t)=V_ {peak} \sin (\omega t)\) 」を、その上の式の「\(V_{AC}\) 」に入れると、「抵抗：\(R\) 」の消費電力を表す式は下記になります。

$$P_{AC} (t)=\displaystyle\frac{(V_{AC})^{2}}{R}=\displaystyle\frac{(V_ {peak} \sin (\omega t))^{2}}{R}$$

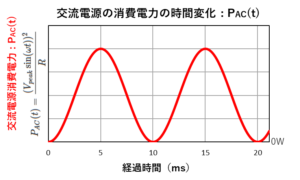
「DC100V」と「AC100V」の消費電力のグラフ

「DC100V」と「AC100V」の消費電力を計算する式が導けましたので、横軸を経過時間にしてグラフ化してみます。

「抵抗値：R=100Ω」、「AC100V」の「周波数：f=50Hz」とすると、「DC100V」と「AC100V」の消費電力の計算式は下記になります。

$$P_{DC100V}=\displaystyle\frac{(V_{DC})^{2}}{R}=\displaystyle\frac{100^{2}}{100}=100$$

$$P_{AC100V} (t) =\displaystyle\frac{(V_ {peak} \sin (\omega t)) ^ {2}}{R}$$

$$=\displaystyle\frac{(141 \sin (2\pi ft)) ^ {2}}{100} $$

$$ =\displaystyle\frac{(141 \sin (2\pi 50t)) ^ {2}}{100} $$

$$=\displaystyle\frac{(141 \sin (100\pi t)) ^ {2}}{100} $$

上の式で計算した消費電力のグラフを、電圧のグラフに並べて置きました。

二つのグラフは、横軸の経過時間をそろえています。

赤色の「AC100V」の線を見ると、上の電圧が1回上下する間に、下の消費電力は2回上下することが分かります。

この消費電力のグラフから、赤色の「\(P_{AC100V} (t)\)」を平均すると、青色の「\(P_{DC100V}\)」と同じになることが視覚的に分かると思います。

今回はあらかじめ「\(V_ {peak}=141V\) 」として、接続した抵抗での消費電力が、「\(DC100V\)」の場合と「\(AC100V\)」の場合で等しくなることを確認しました。

次回は逆に、「\(DC100V\)」と「\(AC100V\)」に接続した抵抗での消費電力が等しくなる場合に、「\(V_ {peak}=141V\) 」になることを計算していきます。

よろしければ以下のバナーをクリックしていただけると励みになります！

にほんブログ村


人気ブログランキング