直流と交流の違い〔６〕（交流の式：Vpeak sin(ωt)）

2023年10月16日 2023年12月15日

講師Kazu

「直流と交流の違い〔３〕」で、「まずは「$V_{AC}(t)$ 」を表す式を求めます。」と書いてずいぶん経ちましたが、今回はその式を求めます。

今回も、前回と同じような絵を使いますが、少し違います。

まずは左の円座標ですが、前回は「半径：1」の単位円でしたが、今回は「半径：約141V」の電圧の円座標です。

それに伴い、右側のグラフの縦軸も電圧になります。

さて、「$V_{AC}(t)$ 」を「時間：$t$ 」で表す式ですが、「直流と交流の違い〔３〕」では縦軸を「$y$ 」、横軸を「$θ$ 」にして下の式が使えそうと書きました。

$$y=\sin\theta$$

この式は、左下の円座標の単位円の「縦軸：$y$ 」の変化を、「横軸：$\theta$ 」で表した右下のグラフの式になります。

この式の「$\theta$ 」を、前回の投稿で書いた「角周波数：$\omega (=2\pi f)$ 」と「時間：$t$ 」で表すと下記になります。

$$y=\sin (\omega t) $$

次に、電圧が変化するAC100Vの最大値と最小値の振れ幅を「$V_ {peak}$ 」とし、これを上の式の両辺に掛けると下記になります。

$$V_{AC}(t)=V_ {peak} \sin (\omega t) $$

これが、右下のグラフの縦軸「$V_{AC}(t)$ 」を「時間：$t$ 」で表す式です。

この式が合っているかを確認するために、具体的な数字を入れて「$V_{AC}(t)$ 」を計算してみます。

例えば、「経過時間：$10ms=0.01s$ 」のときの「$\omega t$ 」は下記になります。

$$\omega t=2\pi ft=2\pi✕50✕0.01=2\pi✕0.5=\pi$$

（$f$：AC100Vの周波数 ⇒ 東日本は50Hz）

「$\omega t$ 」に「$\pi$ 」を入れて「$V_{AC}(t)$ 」を計算すると下記になります。

$$V_{AC}(t)=V_ {peak} \sin (\pi) =141✕0=0(V) $$

「$\omega t$ 」が「$1$ rad（ラジアン）」のときの「$V_{AC}(t)$ 」も計算してみます。

$$V_{AC}(t)=V_ {peak} \sin (1) =141✕0.84147… =119(V)$$

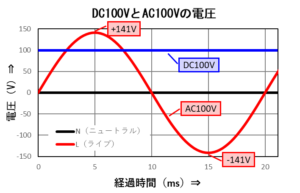
二つの計算結果は、右上のグラフの縦軸の電圧値と一致しています。

次回からは、この「$V_{AC}(t)=V_ {peak} \sin (\omega t) $ 」の式を使って「$V_ {peak}$ 」が「約141V」になることを求めていこうと思います。

よろしければ以下のバナーをクリックしていただけると励みになります！