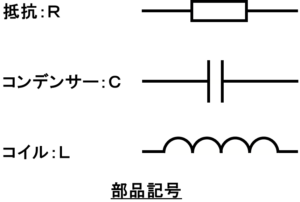
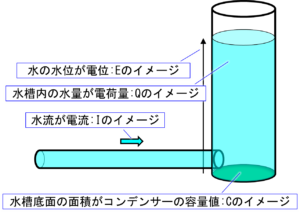
電気回路_コンデンサーの動作【直流】〔１〕

2022年11月21日 2022年11月22日

講師Kazu

コンデンサーの動作を理解するために、まずはコンデンサーに一定の電圧や電流を加えてみます。

コンデンサーの電気記号と、コンデンサーの構造イメージ図を下に示します。

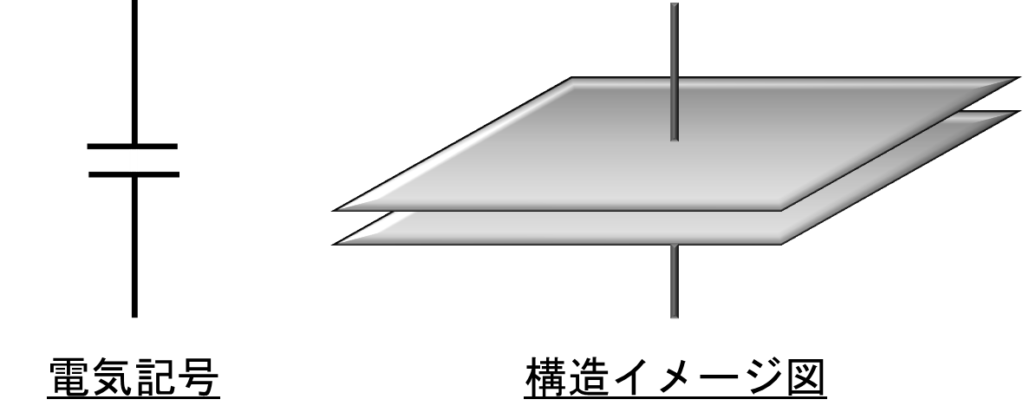
コンデンサーの電気記号と構造イメージ図は、ほぼそのままですね。

コンデンサーの基本構造は、2枚の金属板を接触しないように向かい合わせて置いたものです。

そのため、2枚の金属板の間に電流は流れません。

このコンデンサーの動作を理解するために、まずコンデンサーに定電圧を接続してみます。

回路図で書くと下のようになります。

容量値が「C」のコンデンサーに電圧「E」を接続して、しばらく時間が経過した後の状態を考えます。

その時のコンデンサーの状態を構造イメージ図で表すと、下のようになります。

電圧源のプラスに接続された上側の金属板にはプラスの電気がたまり、マイナスに接続された下側の金属板にはマイナスの電気がたまっています。

プラスとマイナスの電気の間には、磁石のように引っ張り合う力が働くのですが、これをクーロン力といいます。

クーロン力の単位は、以前の投稿（「力」と「エネルギー」の単位）にも書いた「N（ニュートン）」です。

金属板にたまった電気は「電荷」といいますが、「電荷」が大きいほど引っ張り合う力は大きくなります。

また、二つの「電荷」の距離が近づいても引っ張り合う力は大きくなります。

二つの「電荷」の大きさを「q₁」「q₂」、二つの「電荷」の距離を「r」とすると、引っ張り合う力「F」は下の式で求まります。

$$F=k\displaystyle\frac{q_1q_2}{r^2}$$

kは比例定数で、二つの「電荷」の間がどんな物質かで求まります。

例えば二つの「電荷」の間が真空なら、k＝9.0×10⁹になります。

唐突なお願いですが、今後「×10⁹」の表現は、本文中では「E9」と書かせてください。

先ほどのkの値ならk=9.0E9という表現方法で、一般によく使用される書き方です。

さて、話を本題に戻しますが、kの値は下の式で計算できます。

$$k=\displaystyle\frac{1}{4πε_0}=\displaystyle\frac{1}{4×π×8.85×10^{-12}}=9.0×10^9$$

ε₀は真空の誘電率で、8.85E-12です。

εは「イプシロン」といいます。

二つの「電荷」の間が真空以外の場合は、真空の誘電率との比である比誘電率εsを使用して下の式で計算します。

$$F=k\displaystyle\frac{q_1q_2}{ε_sr^2}=\displaystyle\frac{1}{4πε_0}\frac{q_1q_2}{ε_sr^2}=\displaystyle\frac{1}{4πε_0ε_s}\frac{q_1q_2}{r^2}$$

比誘電率εsは通常1以上なので、誘電率は真空の場合が最も小さくなると考えてよいと思います。

εsの位置は右でも左でも同じなので、考えやすい方で良いと思います。

また、最初にコンデンサーの容量値を「C」としましたが、金属板の面積を「S」として、2枚の金属板の距離を「ｄ」とすると、容量値「C」は下の式で求まります。

$$C=\displaystyle\frac{ε_0ε_sS}{d}$$

このコンデンサーに電圧「E」を接続すると、このコンデンサーに蓄えられる電荷「Q」は下の式で求まります。

$$Q=CE$$

今回は、こんなにいろいろな式を書くつもりはなかったのですが、もう少し説明した方が分かりやすいかなと思って書いているうちに、式だらけになりました。すみません。

もともと書く予定だった内容は、今回書いた内容を活用しながら次回書こうと思います。

よろしければ以下のバナーをクリックしていただけると励みになります！