微分や積分の話【積分（２）】

今回こそは飛行機が停止状態から加速し、離陸するときの速度や離陸までの走行距離を、積分の考え方を使って計算してみます。

飛行機の離陸

飛行機が離陸時に加速する様子を、下の図のように想定します。

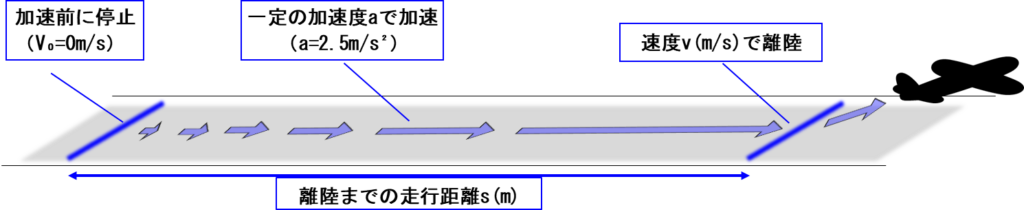
まず、左端の線で飛行機はいったん停止します。

それから、一定の加速度：a=2.5m/s²で加速していくとします。

もしエンジン出力が一定なら加速度は変化すると思いますが、ここでは加速度が一定とさせてください。

加速を始めた飛行機は少しずつ速度を上げて、30秒後に離陸するとします。

その時の走行速度と、離陸までの走行距離を計算しましょう。

離陸時の速度

加速度は一定としたので、30秒後の速度は加速度×経過時間で計算できます。

この計算にも積分の考え方は使えますが、逆に分かりづらくなりそうなので、ここでは単純に掛け算で30秒後までの速度を計算します。

$$v=at=2.5(m/s_2)×30(s)=75(m/s)=270(km/h)$$

・v(m/s)：t秒後の速度（1秒間に一定の方向に進む距離）

・a(m/s²)：加速度（速度が1秒間にa(m/s)ずつ増加）

・t(s)：経過時間（単位は秒）

横軸を経過時間、縦軸を速度とすると、下のグラフで表せます。

縦軸の左側が秒速（赤のトレース）、右側が時速（黒のトレース）で、\(「v=at=2.5t」\)のグラフです。（加速度：a=2.5m/s²なので）

経過時間：0秒時点での速度は0m/s。

経過時間：1秒時点での速度は2.5m/s。

経過時間：10秒時点での速度は25m/s。

経過時間：30秒時点での速度は75m/sになることがグラフからも分かります。

離陸までの走行距離

さて、ここで離陸までの走行距離を計算します。

走行距離（m）は、走行速度（m/s）と走行時間（s）の掛け算で求まります。

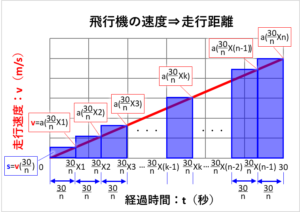
もう一度経過時間を横軸、走行速度を縦軸としたグラフを下に示します。

先ほど書いたように、走行距離は走行速度（縦軸：秒速）に走行時間（横軸：経過時間）を掛けて求めますが、走行速度は時間の経過とともに変化します。

正確な走行距離を計算するためには、変化する走行速度ごとに走行距離を計算して足し合わせる必要があります。

そこで、下のグラフのように横軸の経過時間を細かく刻み、その細かく刻んだ経過時間と、その時の走行速度を掛けて、細かく刻んだ時間の走行距離を求めます。

この掛け算を0秒から30秒まで繰り返し、それらの掛け算の結果を全て足し合わせることで全体の走行距離を求めます。

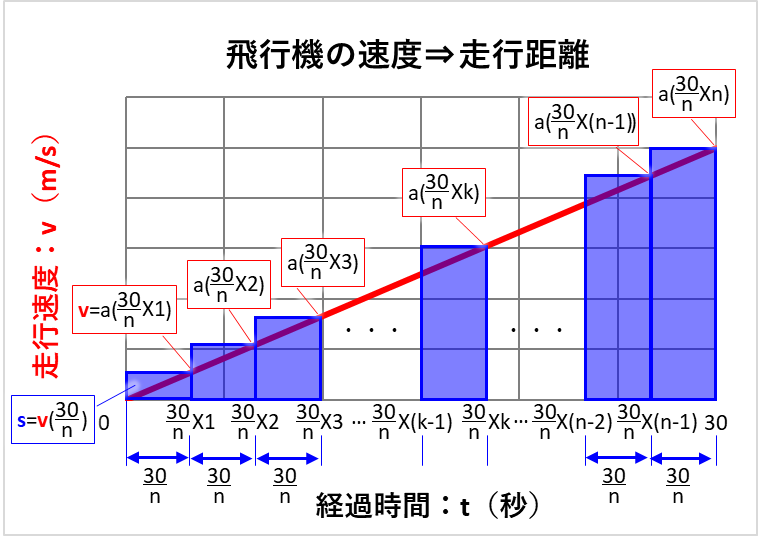
具体的には30秒を「n」等分します。

すると、掛け算に使う時間は全て次の式で表せます。

$$30秒を「n」等分した時間=\displaystyle\frac{30}{n}=Δt$$

上の式のように、30秒を「n」等分した時間：\(\displaystyle\frac{30}{n}\)秒を\(「Δt」\)とします。

そうすると、上のグラフの一番左の四角形の走行速度：\(at_1\)は次の式で計算できます。

$$一番左の四角形の走行速度=at_1=a(Δt×1)$$

左から2個目の四角形の走行速度：\(at_2\)は次の式で計算できます。

$$2個目の四角形の走行速度=at_2=a(Δt×2)$$

左から3個目の四角形の走行速度：\(at_3\)は次の式で計算できます。

$$3個目の四角形の走行速度=at_3=a(Δt×3)$$

次はちょっととばして、左から「k」個目の四角形の走行速度：\(at_k\)は次の式で計算できます。

$$k個目の四角形の走行速度=at_k=a(Δt×k)$$

最後の「n」個目の四角形の走行速度：\(at_n\)は次の式で計算できます。

$$n個目(30秒後)の四角形の走行速度=at_n=a(Δt×n)=a(\displaystyle\frac{30}{n}×n)=a×30$$

これで掛け算する時間と、変化する走行速度は全て式で表せました。

それではちょっと式が長くなりますが、これらの時間と走行距離の掛け算を行い、掛け算した結果を全部足していきます。

$$走行距離=(at_1)Δt+(at_2)Δt+(at_3)Δt+…+(at_k)Δt+…+(at_n)Δt$$

足し合わせる全ての項に\(aΔt\)があるので、全ての項を\(aΔt\)でくくります。

$$=aΔt(t_1+t_2+t_3+…+t_k+…+t_n)$$

ここで、\(t_1=Δt×1\)、\(t_2=Δt×2\)、\(t_3=Δt×3\)、・・・、\(t_k=Δt×k\)、・・・、\(t_n=Δt×n\)を代入します。

$$=aΔt(Δt×1+Δt×2+Δt×3+…+Δt×k+…+Δt×n)$$

カッコ内に出てきた\(Δt\)も、カッコの外に出します。

$$=aΔt^2(1+2+3+…+k+…+n)$$

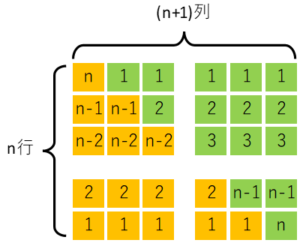
ここで上の式の\(（1+2+…+k+…+n）\)に、前回の投稿に書いた下の公式を代入します。

$$「1からｎまでの総和」=(1+2+…+k+…+n)=\sum_{k=1}^{n} k=\displaystyle\frac{n(n+1)}{2}$$

そうすると「走行距離」の式は下記になります。

$$走行距離=aΔt^2(1+2+3+…+k+…+n)$$

$$=aΔt^2\sum_{k=1}^{n} k=aΔt^2\displaystyle\frac{n(n+1)}{2}$$

\(Δt=\displaystyle\frac{30}{n}\)を代入します。

$$=a\left(\displaystyle\frac{30}{n}\right)^2\displaystyle\frac{n(n+1)}{2}=a\left(30\right)^2\displaystyle\frac{n(n+1)}{2n^2}=a(30)^2\displaystyle\frac{\left(1+\displaystyle\frac{1}{n}\right)}{2}$$

ここで、30秒の分割数\(「n」\)をどんどん大きくして、\(「n→無限大」\)にすると\(「\displaystyle\frac{1}{n}→0」\)になるので、上の式は次のようになります。

$$走行距離=a(30)^2\displaystyle\frac{\left(1+\displaystyle\frac{1}{n}\right)}{2}=a(30)^2\displaystyle\frac{(1+0)}{2}=\displaystyle\frac{1}{2}a(30)^2$$

飛行機は、加速度：a=2.5m/s²で加速するとしていますので、走行距離は次のようになります。

$$走行距離=\displaystyle\frac{1}{2}a(30)^2=\displaystyle\frac{1}{2}2.5(30)^2=1125(m)$$

離陸までの走行距離は、1,125mになりました。

上の計算式の「30」秒を一般化して「t」秒にすると、次の式になります。

$$走行距離=\displaystyle\frac{1}{2}at^2$$

この式を横軸：経過時間、縦軸：走行距離にしてグラフ化すると下記になります。

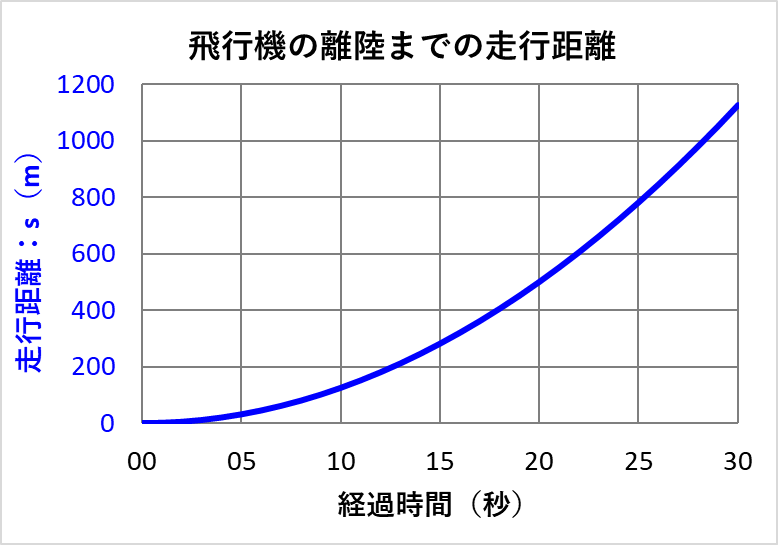
この走行距離の式は、前回の投稿の最初の方に書いた下の式で、\(t=0\)時点での走行速度：\(V_0\)と走行距離：\(S_0\)をゼロにした式になります。

$$移動距離(m)=s=\displaystyle\frac{1}{2}at^2+V_0t+S_0$$

積分との関係について

今回は飛行機が停止した状態から、加速度：2.5m/s²で30秒間加速して離陸するときの速度と走行距離を計算してみました。

ただ、今回はこの計算と積分の関係までは書けませんでした。

次回はこの計算と積分の関係について書こうと思います。

よろしければ以下のバナーをクリックしていただけると励みになります！

にほんブログ村