微分や積分の話【積分(3)】
【積分(2)】が長くなったので、【積分(2)】の計算と積分の関係はこちらに書きます。
まずは、前回投稿【積分(2)】の整理
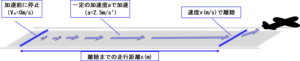
前回の【積分(2)】では、飛行機が離陸するまでの走行距離について書きました。
前回の計算内容を、簡単にまとめてみます。
$$走行距離=(at_1)Δt+(at_2)Δt+(at_3)Δt+…+(at_k)Δt+…+(at_n)Δt$$
$$={\sum_{k=1}^{n} (at_k)}Δt$$
上の「\({\sum (at_k)}Δt\)」は、その上の式に書いたように「\((at_1)Δt\)」から「\((at_n)Δt\)」までを足したものです。
「\({\sum}\)」の下の「\({k=1}\)」と上の「\(n\)」は、「\((at_k)Δt\)」の「\(k\)」に「\(1\)」から「\(n\)」まで順番に入れて、それらの全てを足し合わせるという記号です。
「\(at_k\)」は、加速度「\(a\)」と時間「\(t_k\)」の掛け算なので、「\(t_k\)」経過時点での速度です。
「\((at_k)Δt\)」は、速度「\(at_k\)」に「\(Δt\)」を掛けるので、「\(t_k\)」経過時点で「\(Δt\)」の間に進む走行距離になります。
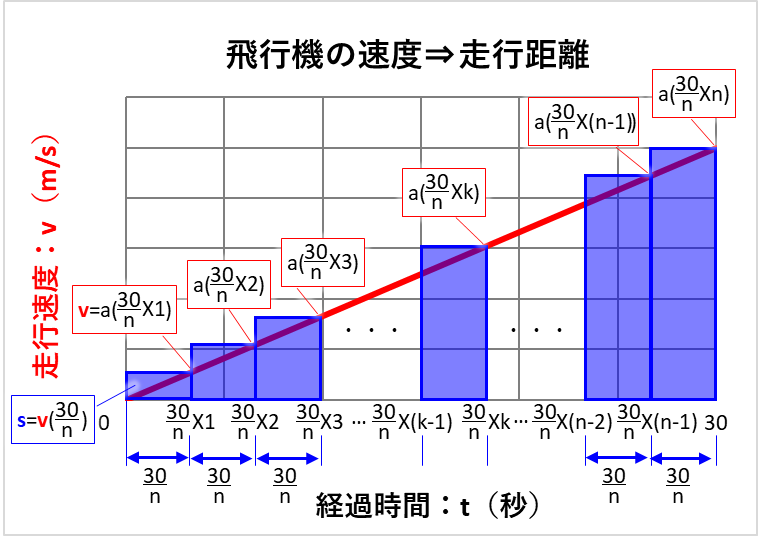
前回投稿のグラフをもう一度下に貼りますが、\(Δt=\displaystyle\frac{t}{n}\)です。
下のグラフでは「\(t=\)30秒」としたので、\(Δt=\displaystyle\frac{t}{n}=\displaystyle\frac{30}{n}\)でした。
走行距離と積分の関係
前回の投稿で、「\({\sum_{k=1}^{n} at_k}Δt\)」の「\(n\)」の数を大きくして、「\(n→∞\)」にすると書きましたが、それを表す記号は「\(\lim_{n \to ∞}\)」になります。
前回の投稿で書いた式の「30秒」⇒「\(t\)」にして、「\(\lim_{n \to ∞}\)」の記号を使った式は下記になるので、これを解いていきます。
$$走行距離=\lim_{n \to ∞}{\sum_{k=1}^{n} at_k}Δt$$
$$=\lim_{n \to ∞}\left((at_1)Δt+(at_2)Δt+(at_3)Δt+…+(at_k)Δt+…+(at_n)Δt\right)$$
$$=\lim_{n \to ∞}aΔt\left(t_1+t_2+t_3+…+t_k+…+t_n\right)$$
$$=\lim_{n \to ∞}aΔt\left(Δt×1+Δt×2+Δt×3+…+Δt×k+…+Δt×n\right)$$
$$=\lim_{n \to ∞}aΔt^2\left(1+2+3+…+k+…+n\right)$$
$$=\lim_{n \to ∞}aΔt^2\displaystyle\frac{n(n+1)}{2}$$
$$=\lim_{n \to ∞}a\left(\displaystyle\frac{t}{n}\right)^2\displaystyle\frac{n(n+1)}{2}$$
$$=\lim_{n \to ∞}at^2\displaystyle\frac{n(n+1)}{2n^2}$$
$$=\lim_{n \to ∞}at^2\displaystyle\frac{\left(1+\displaystyle\frac{1}{n}\right)}{2}$$
$$=at^2\displaystyle\frac{\left(1+0\right)}{2}$$
$$=\displaystyle\frac{1}{2}at^2$$
式と式の間の説明は、前回の【積分(2)】に書いたので省略しています。
この最初の式は、積分の記号「\(\int\)」を使うと下のように表せます。
$$走行距離=\lim_{n \to ∞}{\sum_{k=1}^{n} at_k}Δt=\int{at}\, dt=\displaystyle\frac{1}{2}at^2$$
今回は時間で積分していますので、時間「\(t_1\)」から「\(t_2\)」までの積分の場合は下のように書きます。
$$走行距離=\int_{t_1}^{t_2}{at}\, dt$$
飛行機離陸時の走行距離は、加速開始後0秒から30秒までだったので、「\(t_1=\)0秒」、「\(t_2=\)30秒」となり下の式で表せます。
$$走行距離=\int_{0}^{30}{at}\, dt$$
それでは次の項で、積分を使って走行距離を計算します。
積分を使った走行距離の計算
停止状態から加速度「\(a\)」で加速したときの「\(t\)」秒後の走行速度は「\(at\)」で計算できます。
このときの走行距離は、時間「\(t\)」を細かく分割して、細かく分割した時間ごとの走行距離を計算し、その細かく分割して計算した走行距離を全て足し合わせることで求まります。
この計算方法を、そのまま式に表すと下記になります。
$$走行距離=\lim_{n \to ∞}{\sum_{k=1}^{n} at_k}Δt$$
先ほど書いたように、この式は積分の記号「\(\int\)」を使うと下のように表せます。
$$走行距離=\lim_{n \to ∞}{\sum_{k=1}^{n} at_k}Δt=\int{at}\, dt$$
加速開始後0秒から30秒までの積分の式は下記になります。
$$走行距離=\int_{0}^{30} at \, dt$$
それでは、この式を計算していきます。
上の式の右側の「\(dt\)」は、細かく刻んだ時間「\(dt\)」で積分することを意味しており、加速度「\(a\)」は時間で変化しないので、前にもってくることができます。
加速度「\(a\)」を前にもってくると下記になります。
$$=a\int_{0}^{30} t \, dt$$
次に積分の公式を使うのですが、ここでは「\(t\)」を積分すると「\(\displaystyle\frac{1}{2}t^2\)」になるので、下記になります。
積分の公式は、一部を後で書きます。
$$=a\left[\displaystyle\frac{1}{2}t^2\right]_{0}^{30}$$
ここで、「\(\displaystyle\frac{1}{2}\)」も時間で変化しないので、前にもってきます。
$$=\displaystyle\frac{1}{2}a\left[t^2\right]_{0}^{30}$$
次に「\([\) \(]\)」の中の「\(t\)」に「\(30\)」と「\(0\)」を入れて計算した結果を引き算します。
$$=\displaystyle\frac{1}{2}a({30}^2-{0}^2)$$
あとは、加速度「\(a\)」に「\(2.5\)」(m/s²)を入れて計算します。
$$=\displaystyle\frac{1}{2}×2.5×(900-0)$$
$$=1125(m)$$
この走行距離は前回の投稿の結果と一致しており、加速を始めて30秒間の走行距離になります。
このように積分の公式を使用すると、加速していく飛行機の走行距離を簡単に求めることができます。
積分の公式(一部)
積分の公式で、よく使いそうなものをいくつか書いておきます。
\(\int{x^a}dx=\displaystyle\frac{x^{a+1}}{a+1}+C ({a}\neq{-1})\)
\(\int{\sin{x}}dx=-\cos{x}+C\)
\(\int{\cos{x}}dx=\sin{x}+C\)
\(\int{e^x}dx=e^x+C\)
「\(+C\)」は積分定数とよばれています。
上の「走行距離」の例では、時間「\(t_1\)」から「\(t_2\)」までの間で積分している「定積分」とよばれるものなので「\(+C\)」は不要です。
上の積分の公式では「\(t_1\)」や「\(t_2\)」の無い「不定積分」なので、「\(+C\)」が入っています。
数学的に正確な説明ではないかもしれないので、もし誤りがあれば「お問合せ」からご指摘ください。
よろしければ以下のバナーをクリックしていただけると励みになります!
にほんブログ村