電気回路_コンデンサーのエネルギー〔１〕

前々回の「ドラム缶に蓄えた水の位置エネルギー」と同じ考え方で、今回はコンデンサーに蓄えた電気のエネルギーを計算します。

2週連続で週末に休日出勤や法事の予定が入り、記事が書けませんでした。

もし、この投稿をお待ちだった方がいらっしゃいましたらお待たせしました。

水槽とコンデンサーの類似点

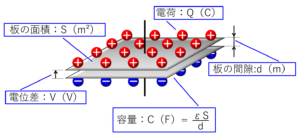
「電気回路_コンデンサーの動作【直流】〔２〕」で使用した絵を下に示しますが、コンデンサーに電荷を蓄えた様子は、容器に水を蓄えた様子ととても良く似ています。

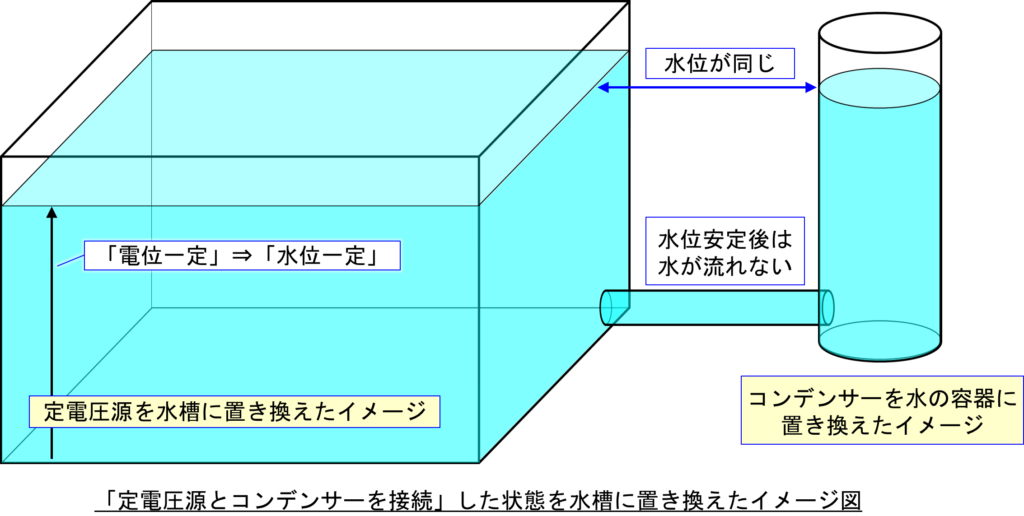
下の図も「電気回路_コンデンサーの動作【直流】〔２〕」で使用した絵ですが、水位は電位、水量は電荷量、水槽底面の面積はコンデンサーの容量（C：キャパシタンス）に相当します。

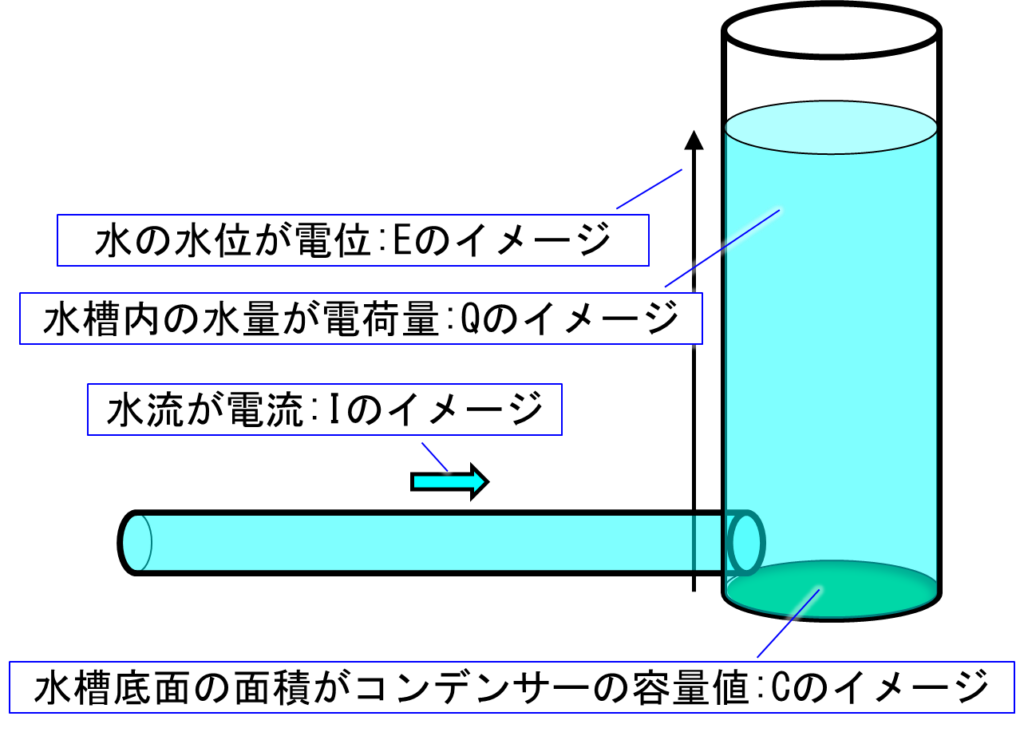
この考え方を使って、コンデンサーに蓄えた電気のエネルギーを計算する式を求めます。

エネルギーの定義

ここで、エネルギー：１ジュール（Ｊ）の定義を書いておきます。

エネルギー：１ジュール（Ｊ）の定義にはいくつかありますが、今回使うのは「位置エネルギー」と「静電エネルギー」の定義です。

【位置エネルギーの定義】

1 ニュートン（N）の力がその力の方向に物体を 1メートル動かすときの仕事

【静電エネルギーの定義】

1 ボルト（V）の電圧の中で 1 クーロン（C） の電荷を動かすのに必要な仕事

この定義は、Wikipediaに書いてありました。

エネルギーの定義を具体的に・・

ちょっと定義が分かりづらいので具体的に書いてみます。

まずは「位置エネルギー」です。

地球上には9.8m/s²の重力加速度がかかっているので、例えば1kgの質量の水は水槽の底を9.8ニュートン（N）の力で押しています。

その力に逆らって、その水を1メートル持ち上げたときの仕事は9.8ジュール（J）です。

これはそのまま、「位置エネルギー」の公式：\(mgh\)です。

次に「静電エネルギー」は、1クーロン（C）の電荷を1ボルト（V）高い電位に移動させる仕事が1ジュール（J）です。

静電エネルギー（仕事）「E」は、電荷を「Q」、電位を「V」とすると、E=QVで求まります。

この「静電エネルギー」の定義から、コンデンサーに蓄えたエネルギーの計算式を求めます。

コンデンサーのエネルギー

コンデンサーの電荷を、容器の水のイメージで考えます。

容器の中が水色だと水っぽいので、電気っぽく黄色にしようと思いましたが、目立たないので赤色にしました。

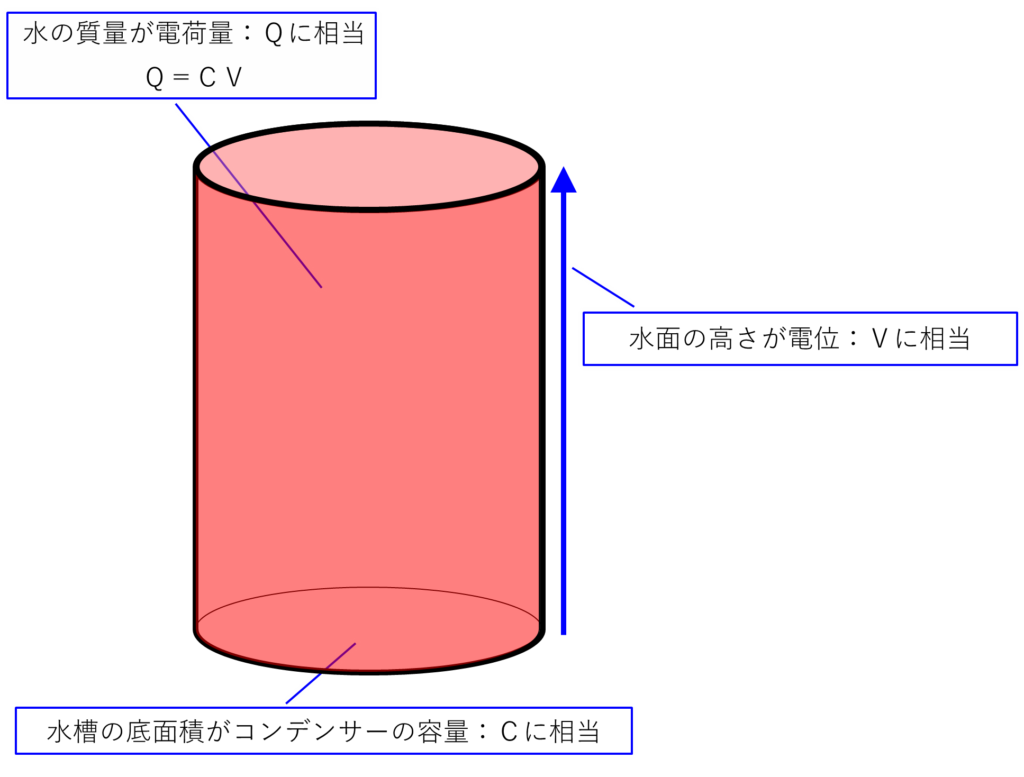
水量は（底面積）✕（水位）で求まりますが、同様に電荷量は（コンデンサーの容量値）✕（電位）で求まります。

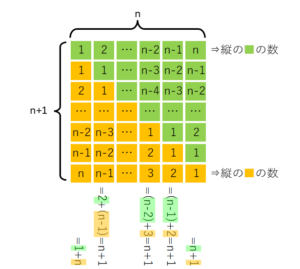
今回も電圧：Vをn分割し、「\(\displaystyle\frac{V}{n}\)」ごとにエネルギーを計算して足していきます。

まずはn分割した一段目のエネルギーのイメージ図です。

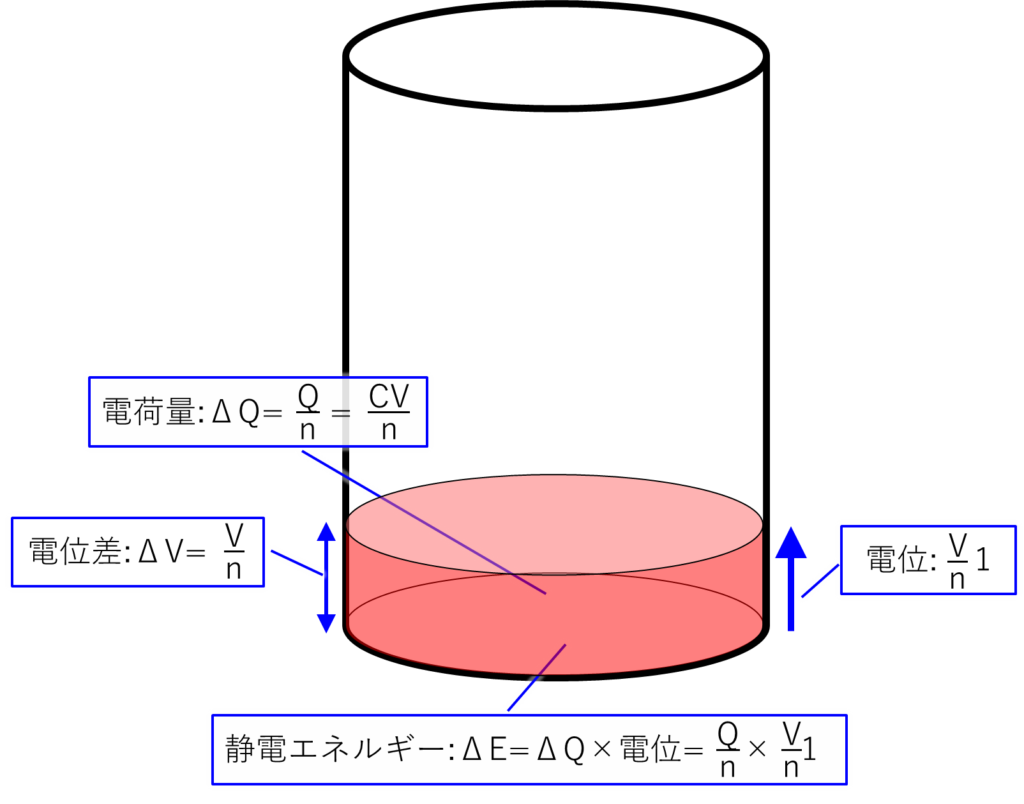
電荷量：ΔQは、底面積に相当する「コンデンサーの容量値：C」と、水面までの高さのn分割に相当する「\(\displaystyle\frac{V}{n}\)」の掛け算「\(C\displaystyle\frac{V}{n}\)」で求まります。

一段目の水面の高さに相当する電位：\(V_1\)は、一段目の上の端の「\(\displaystyle\frac{V}{n}✕1\)」とします。

そうすると、一段目のエネルギー：\(ΔE_1\)は下の式で求まります。

$$ΔE_1=ΔQ✕V_1=C\displaystyle\frac{V}{n}✕\displaystyle\frac{V}{n}✕1=C\displaystyle\frac{V^2}{n^2}✕1$$

次はn分割の下から二段目のエネルギーのイメージ図です。

一段目と同じように考えると、二段目のエネルギー：\(ΔE_2\)は下の式で求まります。

$$ΔE_2=ΔQ✕V_2=C\displaystyle\frac{V}{n}✕\displaystyle\frac{V}{n}✕2=C\displaystyle\frac{V^2}{n^2}✕2$$

次はn分割の下からk段目のエネルギーのイメージ図です。

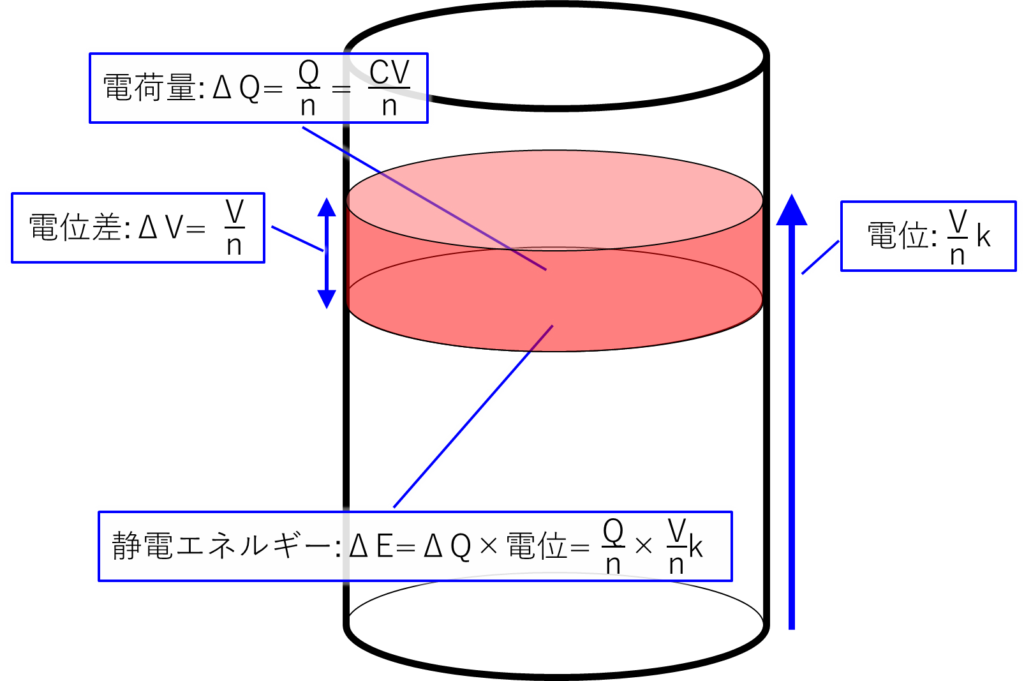
一段目と同じように考えると、k段目のエネルギー：(ΔE_k)は下の式で求まります。

$$ΔE_k=ΔQ✕V_k=C\displaystyle\frac{V}{n}✕\displaystyle\frac{V}{n}✕k=C\displaystyle\frac{V^2}{n^2}✕k$$

次はn分割の下からn段目のエネルギーのイメージ図です。

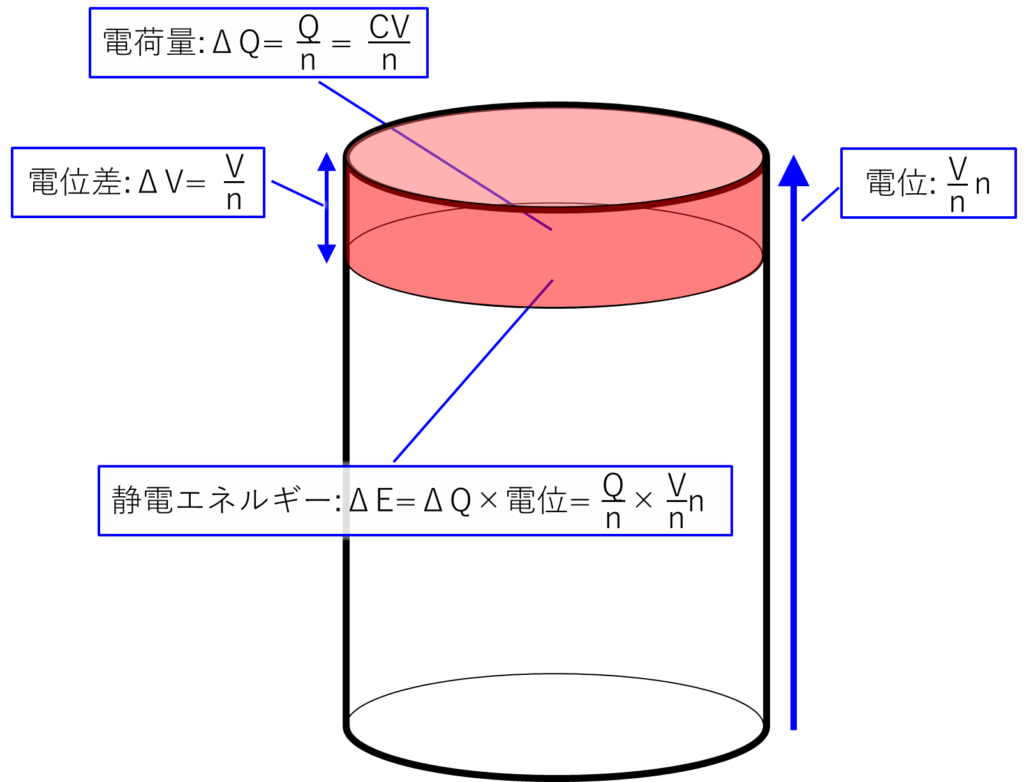
一段目と同じように考えると、n段目のエネルギー：(ΔE_n)は下の式で求まります。

$$ΔE_n=ΔQ✕V_n=C\displaystyle\frac{V}{n}✕\displaystyle\frac{V}{n}✕n=C\displaystyle\frac{V^2}{n^2}✕n$$

それでは、一段目からn段目までのエネルギーを足していき、最後にnを無限大にします。

$$E=\lim_{n \to ∞} \left(C\displaystyle\frac{V^2}{n^2}✕1+C\displaystyle\frac{V^2}{n^2}✕2+…+C\displaystyle\frac{V^2}{n^2}✕k+…+C\displaystyle\frac{V^2}{n^2}✕n\right)$$

$$=\lim_{n \to ∞} \left(C\displaystyle\frac{V^2}{n^2}✕(1+2+…+k+…+n\right)$$

$$=\lim_{n \to ∞} \left(C\displaystyle\frac{V^2}{n^2}✕\displaystyle\frac{n(n+1)}{2}\right)$$

$$=\lim_{n \to ∞} \left(\displaystyle\frac{1}{2}CV^2✕\left(1+\displaystyle\frac{1}{n}\right)\right)$$

$$= \displaystyle\frac{1}{2}CV^2$$

今回は\(ΔQ\)を\(C\displaystyle\frac{V}{n}\)として計算式を求めましたが、\(ΔQ\)を\(\displaystyle\frac{Q}{n}\)として計算式を求めると下記になります。

$$E= \displaystyle\frac{1}{2}QV$$

二つの式は、\(Q=CV\)でも簡単に変換できるので、状況で使い分けることができます。

よろしければ以下のバナーをクリックしていただけると励みになります！

にほんブログ村